t1 x11 x12 x123 t2 x21 x22 x23
1 8.77 9.17 9.21 7.94 8.77 8.96 8.22 9.14
2 9.42 9.99 8.45 9.82 9.42 9.54 8.53 10.20
3 10.98 11.52 10.74 10.70 10.98 12.37 11.02 9.56
4 10.22 9.51 12.00 9.15 10.22 8.85 10.93 10.88
5 11.47 11.81 10.51 12.07 11.47 9.43 14.06 10.90Reliability and Classical Test Theory
PSYC 520
Learning Objectives
- Explain the importance of reliability in measurement
- Explain what true score and error score are in classical test theory (CTT)
- Define and derive reliability in CTT
- Explain what parallel, tau-equivalent, and congeneric tests are
Reliability
A test is reliable means that we would obtain very similar scores if we were to repeat the test

aka dependability or consistency across some condition
Also precision
E.g., across time, items, forms, raters
Reliability concerns observed scores
Reliability coefficient is not defined for a single score, but a set of (hypothetical) scores
On the other hand, precision can be defined for each score
What is Considered Error?
Variability in scores is not necessarily error
E.g., variations in measurement of a person’s weight vs. height across days
What about when an examinee answer a question incorrectly first, and then answer the same question correctly in a second try? Should we consider the difference in response in the two trials “error”?
Classical Test Theory
\[X = T + E\]
- \(X\): Observed score
- \(E\): Random error/inconsistencies
- \(T\): “True” score
- A hypothetical average score if we could repeatedly test a person, and “brainwash” them after each testing
Propensity Distribution (PD)
See Figure 7.1
Standard deviation of PD = standard error of measurement
Random vs. Systematic Error
CTT assumes random error: \(E_1\), \(E_2\), . . . are independent
- Errors are also random across persons
In practice, error can be systematic
- E.g., raters are too lenient; blood pressure meter not calibrated
True Score and Error Score
CTT defines \(T\) = \(\mathop{\mathrm{\mathbb{E}}}(X)\)
So \(T\) can contain systematic error
By construction of CTT
- The expected value of \(E\) is zero
- Corr(\(E\), \(T\)) = 0
Reliability in CTT
- \(\sigma^2_T\) = variance of \(T\) across persons
- \(\sigma^2_X\) = variance of \(X\) across persons
\[ \rho_{X X'} = \frac{\sigma^2_T}{\sigma^2_X} \]
Note
Reliability in CTT is sample-specific
Because \(T\) is not observed, \(\rho_{X X'}\) cannot be obtained
This is solved using the concept of parallel tests
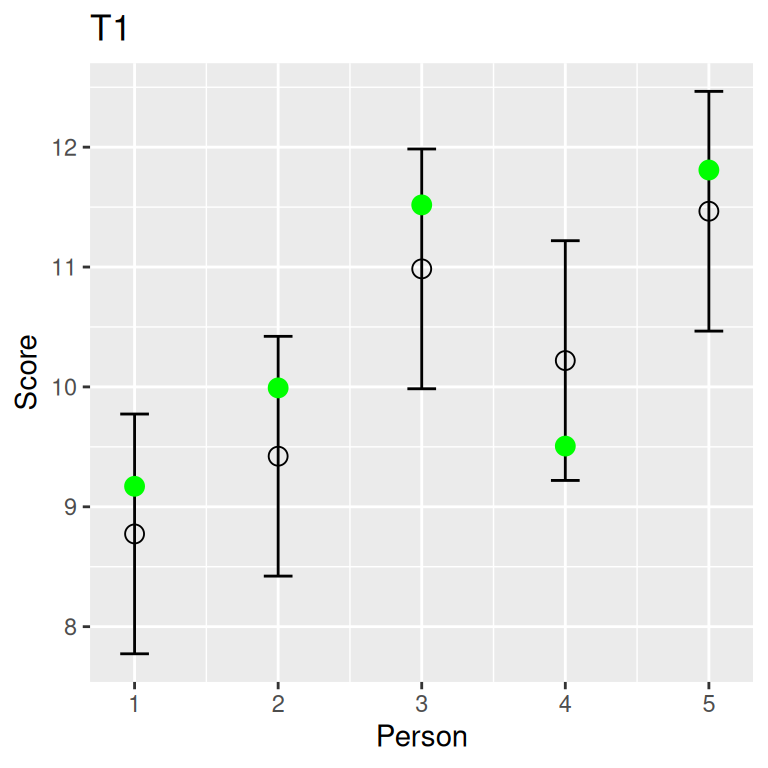
Parallel Tests
If \(X_1\) and \(X_2\) are two parallel tests with true scores \(T_1\) and \(T_2\), they are parallel if and only if
\(T_1\) = \(T_2\); \(\mathop{\mathrm{\mathrm{Var}}}(E_1)\) = \(\mathop{\mathrm{\mathrm{Var}}}(E_2)\)
Without loss of generality, assume \(X_1\) and \(X_2\) have been centered
\[ \mathop{\mathrm{\mathbb{E}}}(X_1 X_2) = \mathop{\mathrm{\mathbb{E}}}(T_1 T_2) + \mathop{\mathrm{\mathbb{E}}}(T_1 E_2) + \mathop{\mathrm{\mathbb{E}}}(T_2 E_1) + \mathop{\mathrm{\mathbb{E}}}(E_1 E_2) \]
The last three terms are zero by construction
Because \(T_1\) = \(T_2\) = \(T\), and \(\mathop{\mathrm{\mathbb{E}}}(T)\) = 0,
\[ \mathop{\mathrm{\mathbb{E}}}(X_1 X_2) = \mathop{\mathrm{\mathbb{E}}}(T^2) = \sigma^2_T \]
With parallel tests, \(\mathop{\mathrm{\mathrm{Var}}}(X_1)\) = \(\mathop{\mathrm{\mathrm{Var}}}(X_2)\) = \(\sigma^2_X\), so
\[ \rho_{X X'} = \frac{\sigma^2_T}{\sigma^2_X} = \frac{\mathop{\mathrm{\mathbb{E}}}(X_1 X_2)}{\sqrt{\mathop{\mathrm{\mathrm{Var}}}(X_1) \mathop{\mathrm{\mathrm{Var}}}(X_2)}} \]
where the last term is the correlation between \(X_1\) and \(X_2\)
So,
Reliability = Correlation between two parallel tests
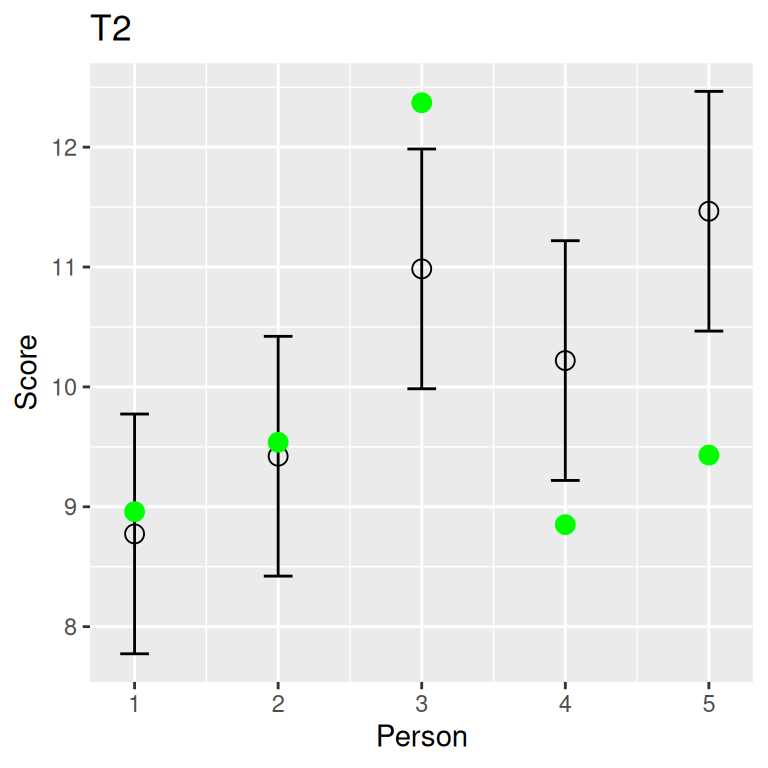
Tau-Equivalent Tests
\(T_1\) = \(T_2\); \(\mathop{\mathrm{\mathrm{Var}}}(E_1)\) may be different from \(\mathop{\mathrm{\mathrm{Var}}}(E_2)\)
t1 x11 x12 x123 t2 x21 x22 x23
1 8.77 8.01 9.05 9.26 8.77 10.57 11.82 3.92
2 9.42 8.80 9.33 10.14 9.42 12.44 10.18 5.65
3 10.98 10.01 12.44 10.51 10.98 14.08 11.37 7.51
4 10.22 12.59 8.85 9.22 10.22 8.65 8.39 13.62
5 11.47 10.75 11.30 12.34 11.47 14.83 6.09 13.48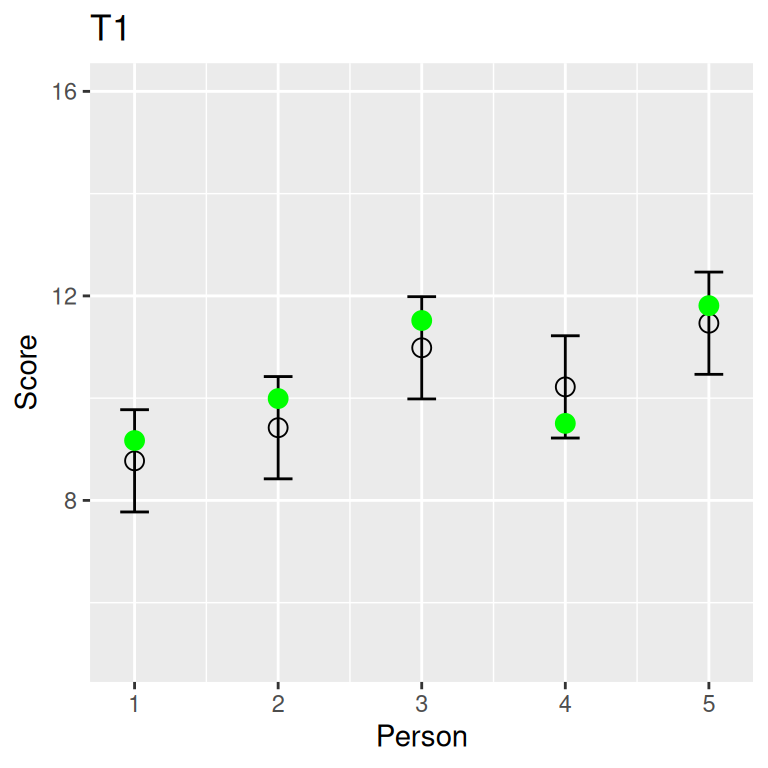
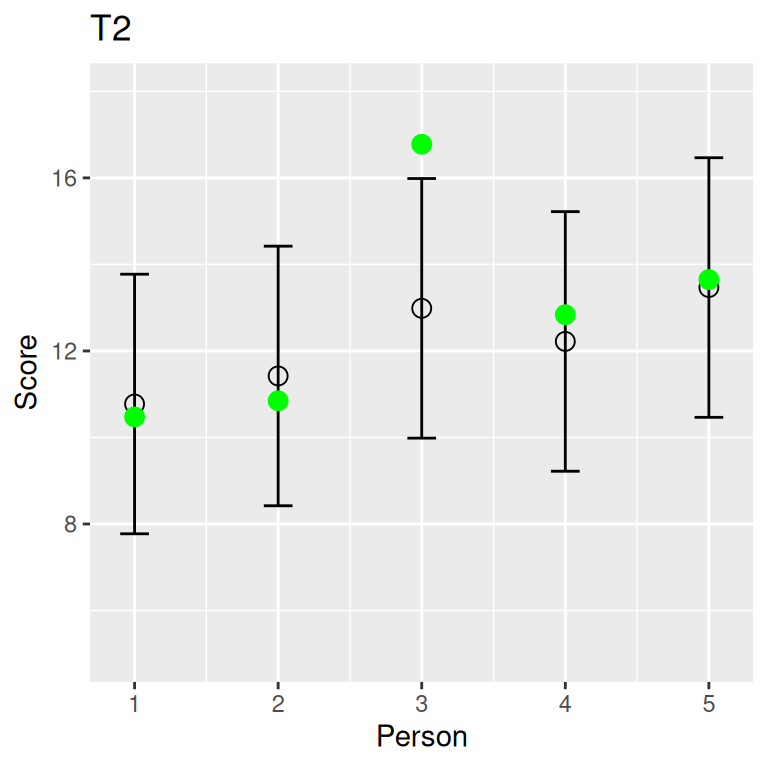
Essentially Tau-Equivalent Tests
\(T_1\) = \(a\) + \(T_2\); \(\mathop{\mathrm{\mathrm{Var}}}(E_1)\) may be different from \(\mathop{\mathrm{\mathrm{Var}}}(E_2)\)
t1 x11 x12 x123 t2 x21 x22 x23
1 8.77 8.56 8.41 9.35 10.77 10.47 12.11 9.74
2 9.42 9.36 8.99 9.91 11.42 10.85 12.62 10.80
3 10.98 10.67 11.02 11.27 12.98 16.78 11.17 11.01
4 10.22 10.72 10.08 9.86 12.22 12.84 8.27 15.56
5 11.47 12.27 10.45 11.67 13.47 13.65 12.40 14.34
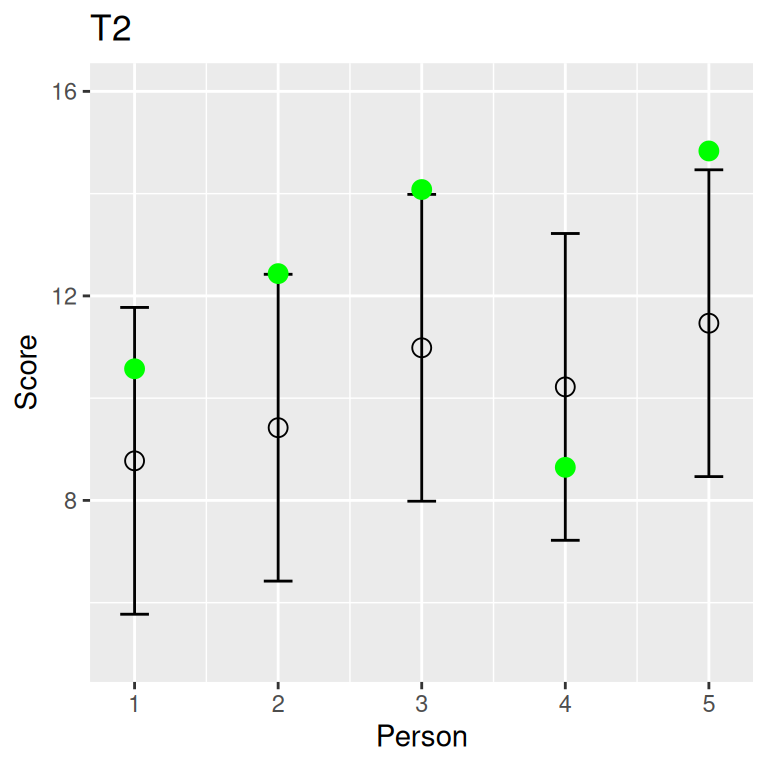
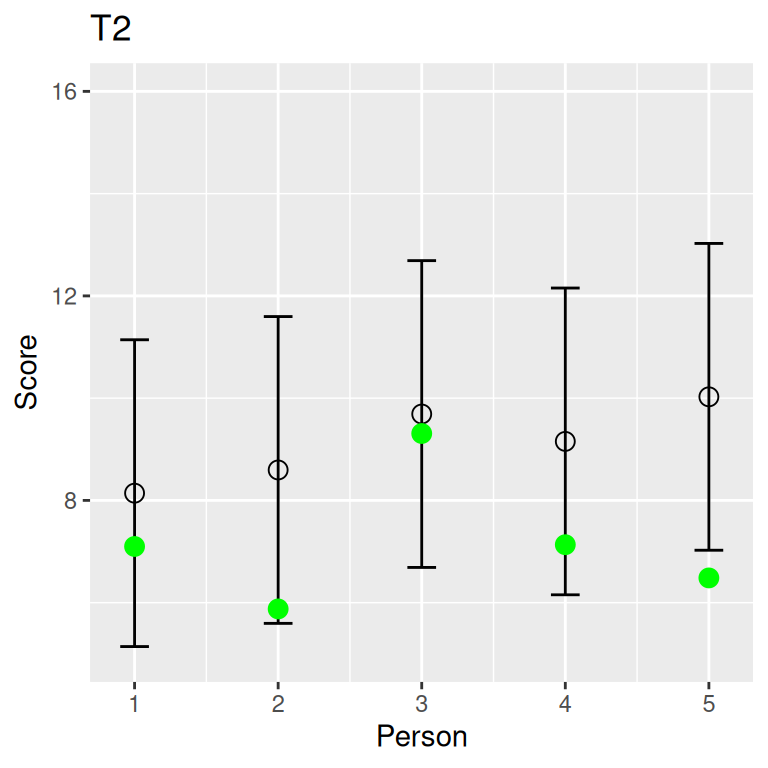
Congeneric Tests
\(T_1\) = \(a\) + \(\color{red}{b}\) \(T_2\); \(\mathop{\mathrm{\mathrm{Var}}}(E_1)\) may be different from \(\mathop{\mathrm{\mathrm{Var}}}(E_2)\)
t1 x11 x12 x123 t2 x21 x22 x23
1 8.77 9.45 8.14 8.73 8.14 7.10 5.59 11.74
2 9.42 7.39 10.54 10.34 8.60 5.88 12.82 7.09
3 10.98 10.77 11.08 11.10 9.69 9.31 10.42 9.34
4 10.22 9.04 10.48 11.13 9.15 7.13 11.24 9.09
5 11.47 11.91 11.23 11.25 10.03 6.48 14.66 8.94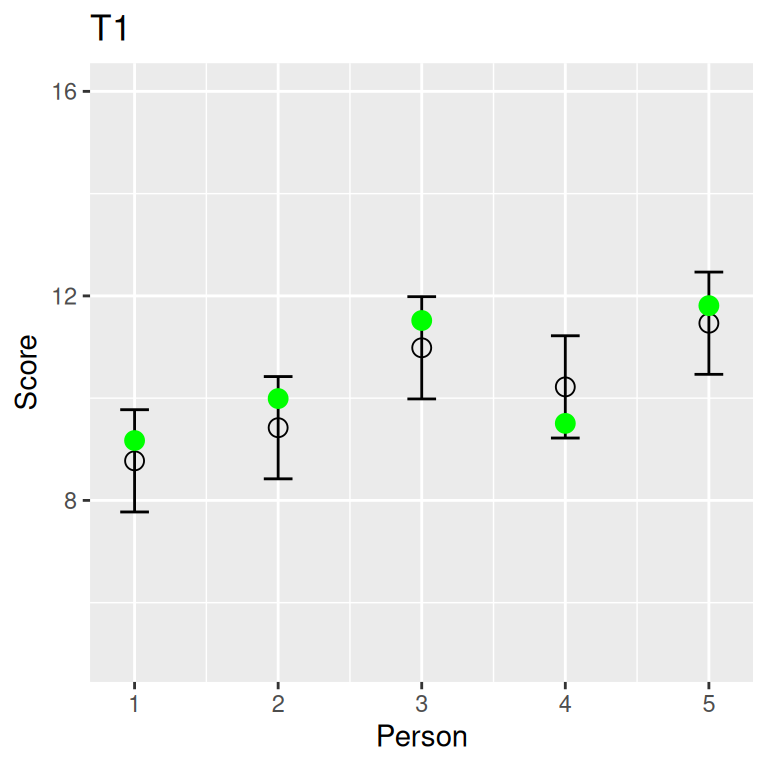
Additional Note on Reliability in CTT
Theoretically speaking, \(0 \leq \rho_{X X'} \leq 1\)
\(\rho_{X X'}\) = squared correlation between \(T\) and \(X\) (think of \(R^2\))
Only one error variance is estimated, which is the average of error variance across persons