Exercise 1

Author

Instructor of PSYC 573

Introduction

In this analysis, we will run a Bayesian analysis to estimate the death rate of patients diagnosed with AIDS in Australia. Let’s start by loading the packages we’ll use for the analysis.

library(tidyverse)  # for data wrangling and visualization
library(knitr)      # for tables
library(posterior)  # for summarizing Bayesian analyses
data(Aids2, package = "MASS")

We present the results of exploratory data analysis in Section 2 and the regression model in Section 3. See

Exploratory data analysis

The data contains 2843 participants.

Summary statistics

Table 1 displays basic summary statistics.

table(Aids2$state, Aids2$status) |>
  kable()
Table 1: Patient status by state
A D
NSW 664 1116
Other 107 142
QLD 78 148
VIC 233 355

Modeling

We can fit a simple linear regression model of the form shown in ?@eq-slr.

Table 2 shows the regression output for this model.

prior_a <- 2
prior_b <- 2

posterior_a <- prior_a + sum(Aids2$status == "D")
posterior_b <- prior_b + sum(Aids2$status == "A")

posterior_draws <- rbeta(4000, shape1 = posterior_a, shape2 = posterior_b)

list(theta = posterior_draws) |>
  summarize_draws() |>
  kable(digits = 2)
Table 2: Summary of posterior distribution of death rate among patients diagnosed with AIDS in Australia
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
theta 0.62 0.62 0.01 0.01 0.6 0.63 1 4114.48 3343.17

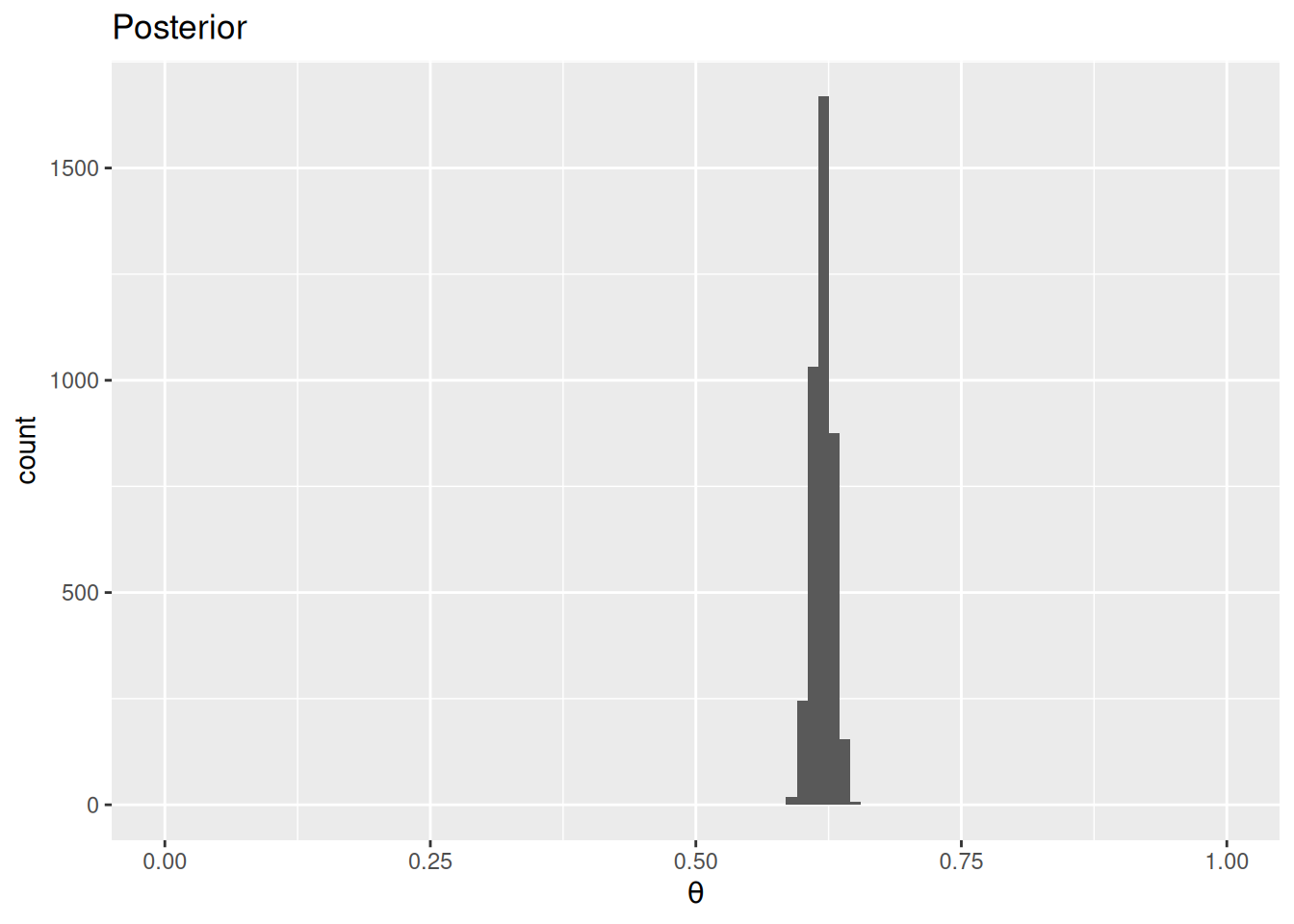
Figure 1 shows the prior and the posterior distributions of the death rate.

prior_draws <- rbeta(4000, shape1 = prior_a, shape2 = prior_b)
ggplot(data.frame(theta = prior_draws), aes(x = theta)) +
  geom_histogram(binwidth = 0.03) +
  labs(title = "Prior", x = expression(theta)) +
  scale_x_continuous(limits = c(0, 1), oob = scales::oob_keep)

ggplot(data.frame(theta = posterior_draws), aes(x = theta)) +
  geom_histogram(binwidth = 0.01) +
  labs(title = "Posterior", x = expression(theta)) +
  scale_x_continuous(limits = c(0, 1), oob = scales::oob_keep)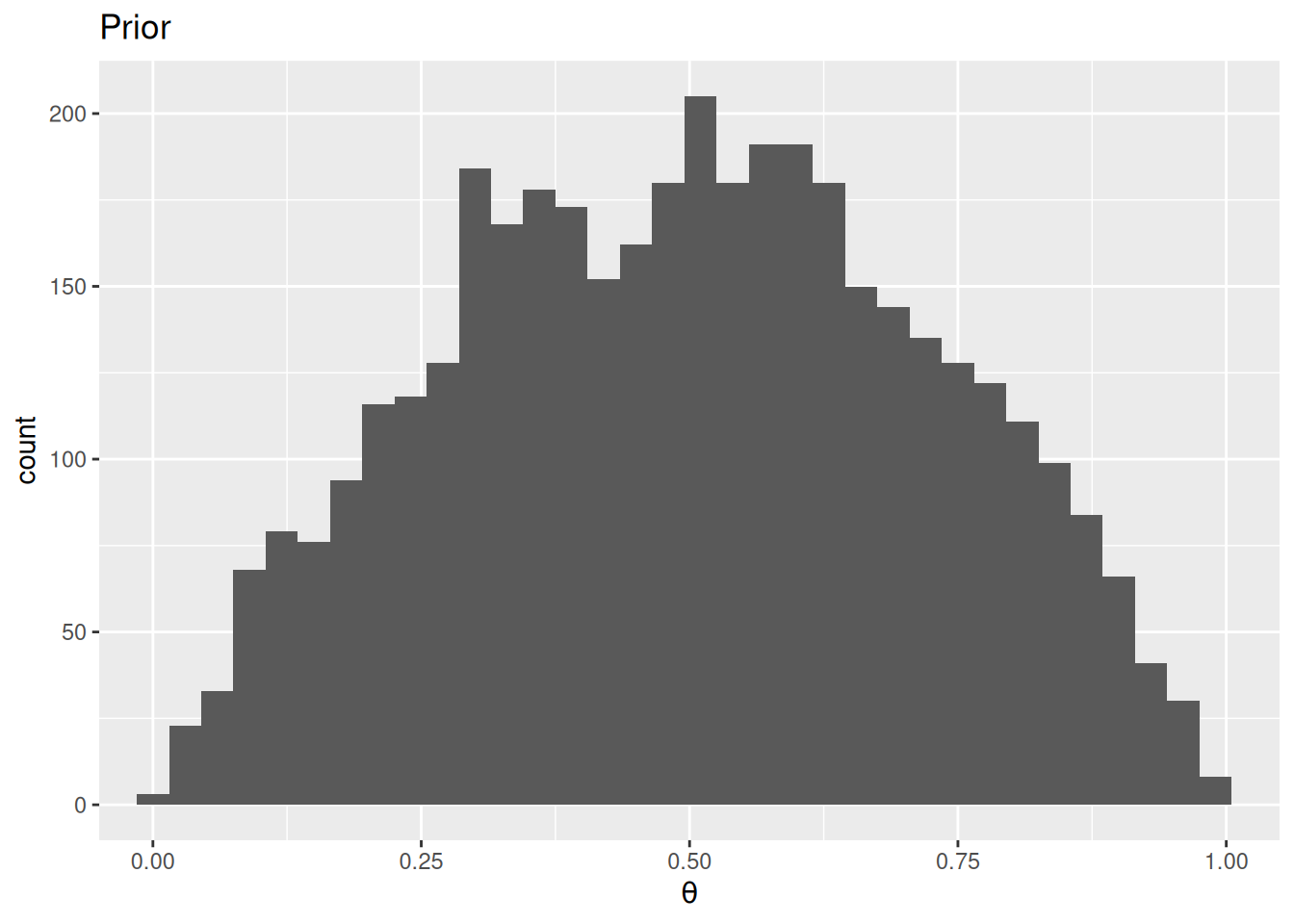
(a) Prior distribution
(b) Posterior distribution
Figure 1: Histograms of prior and posterior distributions of death rate

Results

The estimated death rate is 0.62, 95% CI [0.6, 0.64].

References