| Person | Math Attitude | Y (if T = 1) | Y (if T = 0) | Y(1) - Y(0) |
|---|---|---|---|---|
| 1 | 4 | 75 | 70 | 5 |
| 2 | 7 | 80 | 88 | -8 |
| 3 | 3 | 70 | 75 | -5 |
| 4 | 9 | 90 | 92 | -2 |
| 5 | 5 | 85 | 82 | 3 |
| 6 | 6 | 82 | 85 | -3 |
| 7 | 8 | 95 | 90 | 5 |
| 8 | 2 | 78 | 78 | 0 |
| Average | 5.5 | 81.875 | 82.5 | -0.625 |
Causal Inference
PSYC 573
Causation
Data are profoundly dumb about causal relationships
— Pearl and Mackenzie (2020)
Outline
- Thought experiments
- Potential outcomes
- Causal diagrams
- Mediation
Causal Inference
Obtaining an estimate of the causal effect of one variable on another
an hour more exercise per day causes an increase in happiness by 0.1 to 0.2 points
- Intervention: if I exercise one hour more, my happiness will increase by 0.1 to 0.2 points
- Counterfactual: had I exercised one less hour, my happiness would have been 0.1 to 0.2 points less
Potential Outcomes
\(T\) is the binary treatment variable (e.g., new drug for boosting stat knowledge)
Average Treatment Effect (ATE)
\[ \text{ATE} = \bar Y(1) - \bar Y(0) \]
Observed Outcomes
Only one potential outcome is observed for each person
E.g., Persons 2, 4, 6, 7 take the drug
| Person | T | Math Attitude | Y (if T = 1) | Y (if T = 0) |
|---|---|---|---|---|
| 1 | 0 | 4 | 70 | |
| 2 | 1 | 7 | 80 | |
| 3 | 0 | 3 | 75 | |
| 4 | 1 | 9 | 90 | |
| 5 | 0 | 5 | 82 | |
| 6 | 1 | 6 | 82 | |
| 7 | 1 | 8 | 95 | |
| 8 | 0 | 2 | 78 | |
| average | 5.5 | 86.75 | 76.25 |
Directed Acyclic Graph
Allows researchers to encode causal assumptions of the data
- Based on knowledge of the data and the variables
Data from the 2009 American Community Survey (ACS)
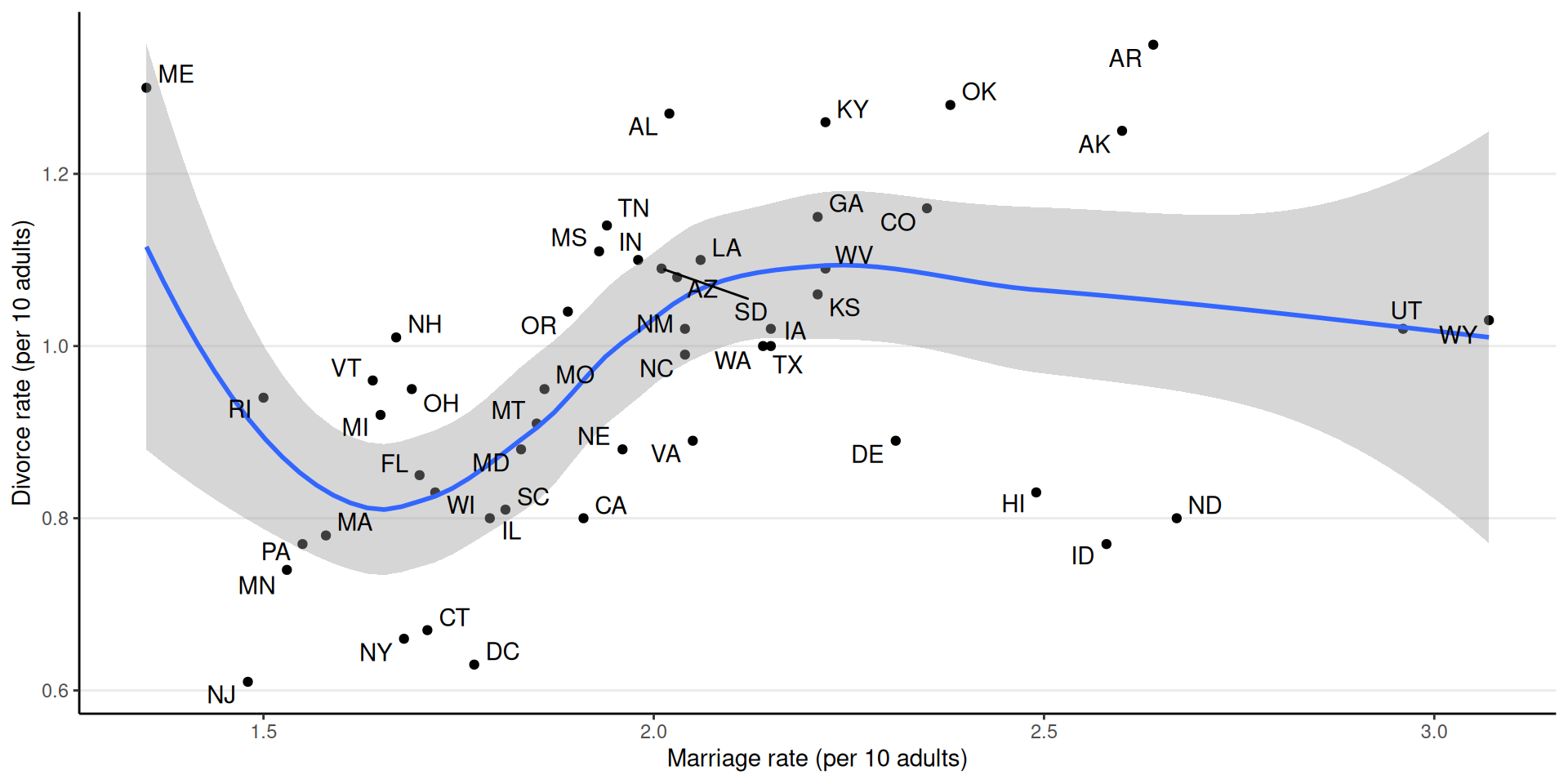
Does marriage cause divorce?
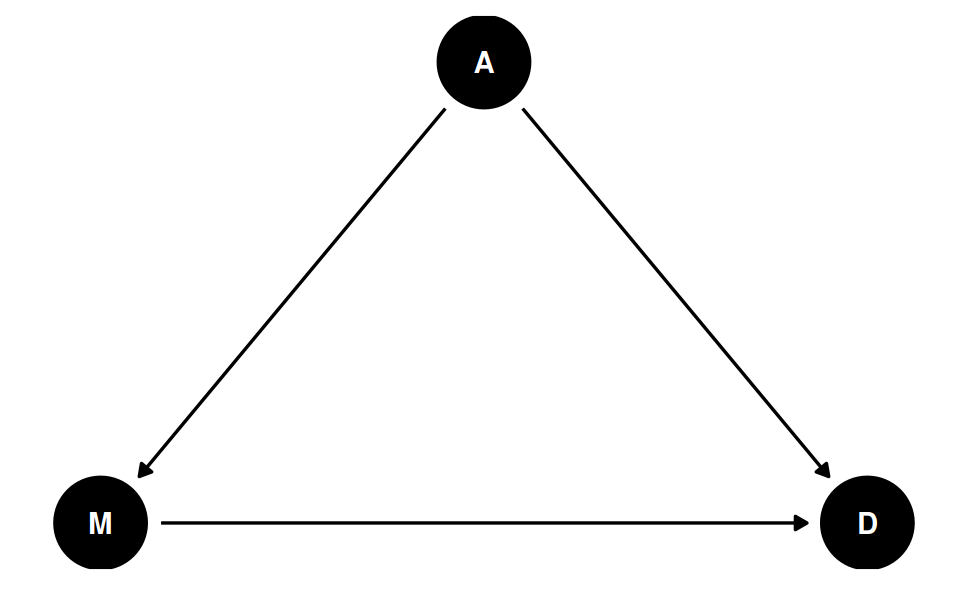
- A = Median age of marriage
- M = Marriage rate
- D = Divorce rate
“Weak” assumptions
- A may directly influence M
- A may directly influence D
- M may directly influence D
“Strong” assumptions
Absence of a link
- E.g., M does not directly influence A
- E.g., A is the only relevant variable in the causal pathway M → D
Basic Types of Junctions
Fork: A ← B → C
Chain/Pipe: A → B → C
Collider: A → B ← C
Fork
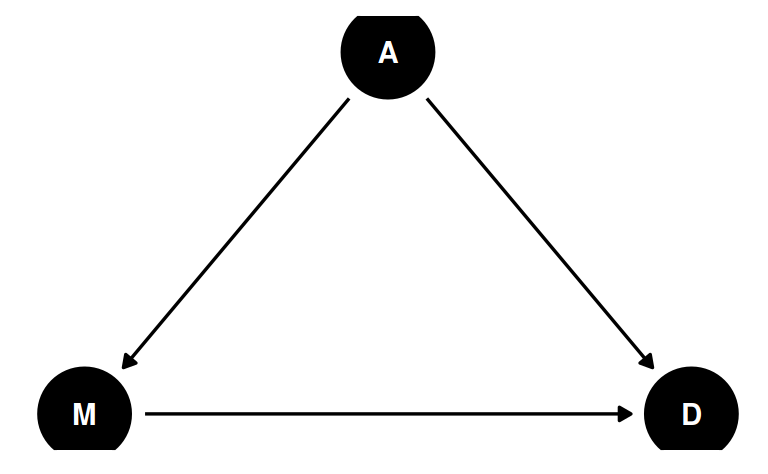
aka Classic confounding
- Confound: something that misleads us about a causal influence
M ← A → D
Assuming the DAG is correct,
- the causal effect of M → D can be obtained by holding constant A
- stratifying by A; “controlling” for A
Pedicting an Intervention
What would happen to the divorce rate if we encourage more people to get married, so that marriage rate increases by 1 per 10 adults?
Based on our DAG, this should not change the median marriage age
Randomization
Removing incoming path to the “causal” variable
Framing Experiment
- X: exposure to a negatively framed news story about immigrants
- Y: anti-immigration political action
No Randomization
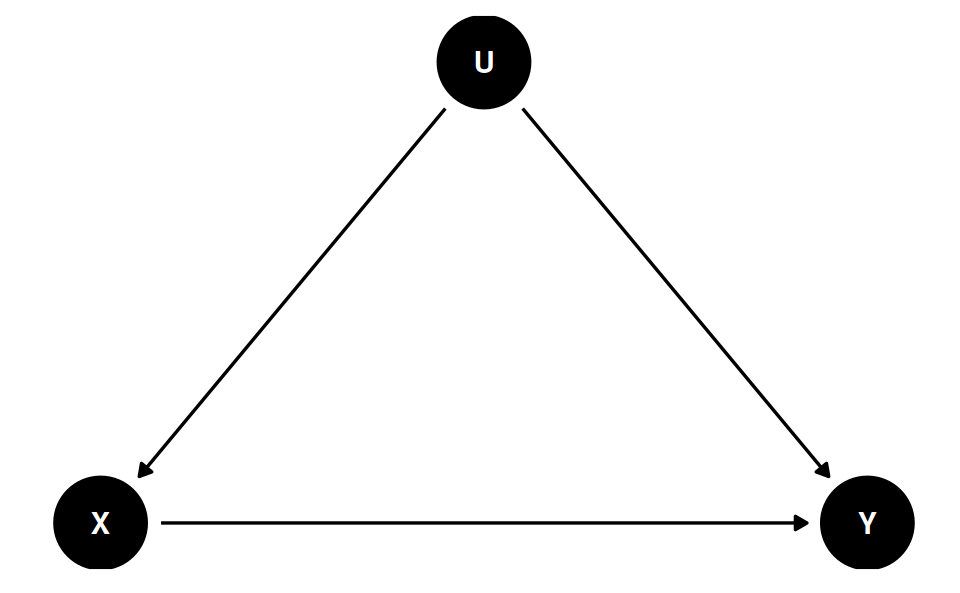
Randomization
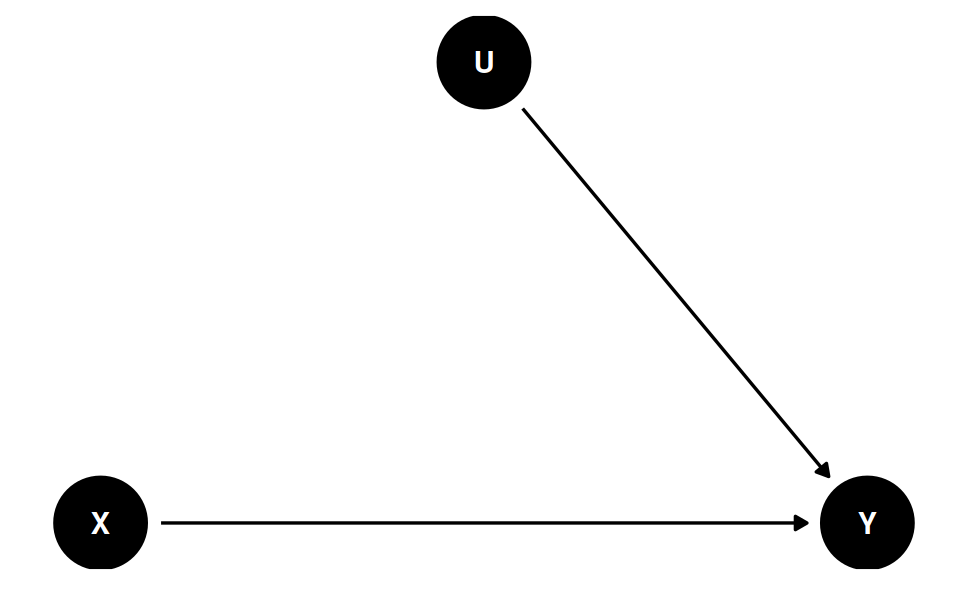
Back-Door Criterion
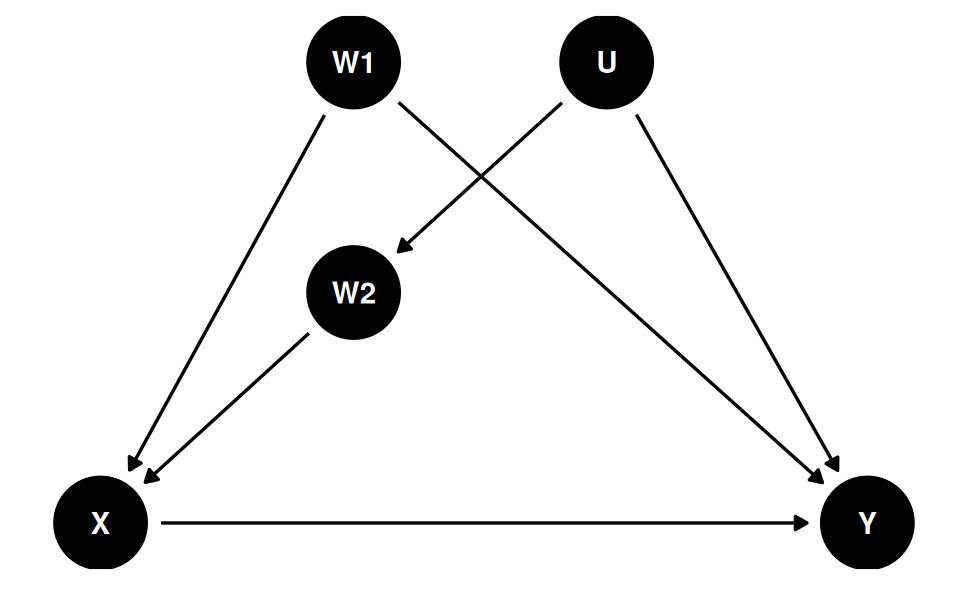
The causal effect of X → Y can be obtained by blocking all the backdoor paths that do not involve descendants of X
- Randomization: (when done successfully) eliminates all paths entering X
- Conditioning (holding constant)
Dagitty
Post-Treatment Bias
Adjusting/“controlling” for covariates imply a causal interpretation
Please do not simply adjust for a variable without thinking about it (especially variables that may be impacted by the treatment)
Data for Framing Experiment
cong_mesg: binary variable indicating whether or not the participant agreed to send a letter about immigration policy to his or her member of Congressemo: post-test anxiety about increased immigration (0-9)tone: framing of news story (0 = positive, 1 = negative)
Results
| No adjustment | Adjusting for feeling | |
|---|---|---|
| b_Intercept | −0.81 [−1.17, −0.44] | −2.01 [−2.64, −1.45] |
| b_tone | 0.21 [−0.30, 0.73] | −0.14 [−0.70, 0.43] |
| b_emo | 0.32 [0.21, 0.43] | |
| R2 | 0.003 | 0.143 |
Which one estimates the causal effect of tone?
Mediation
Mediation is a causal analysis, by definition
Mediation
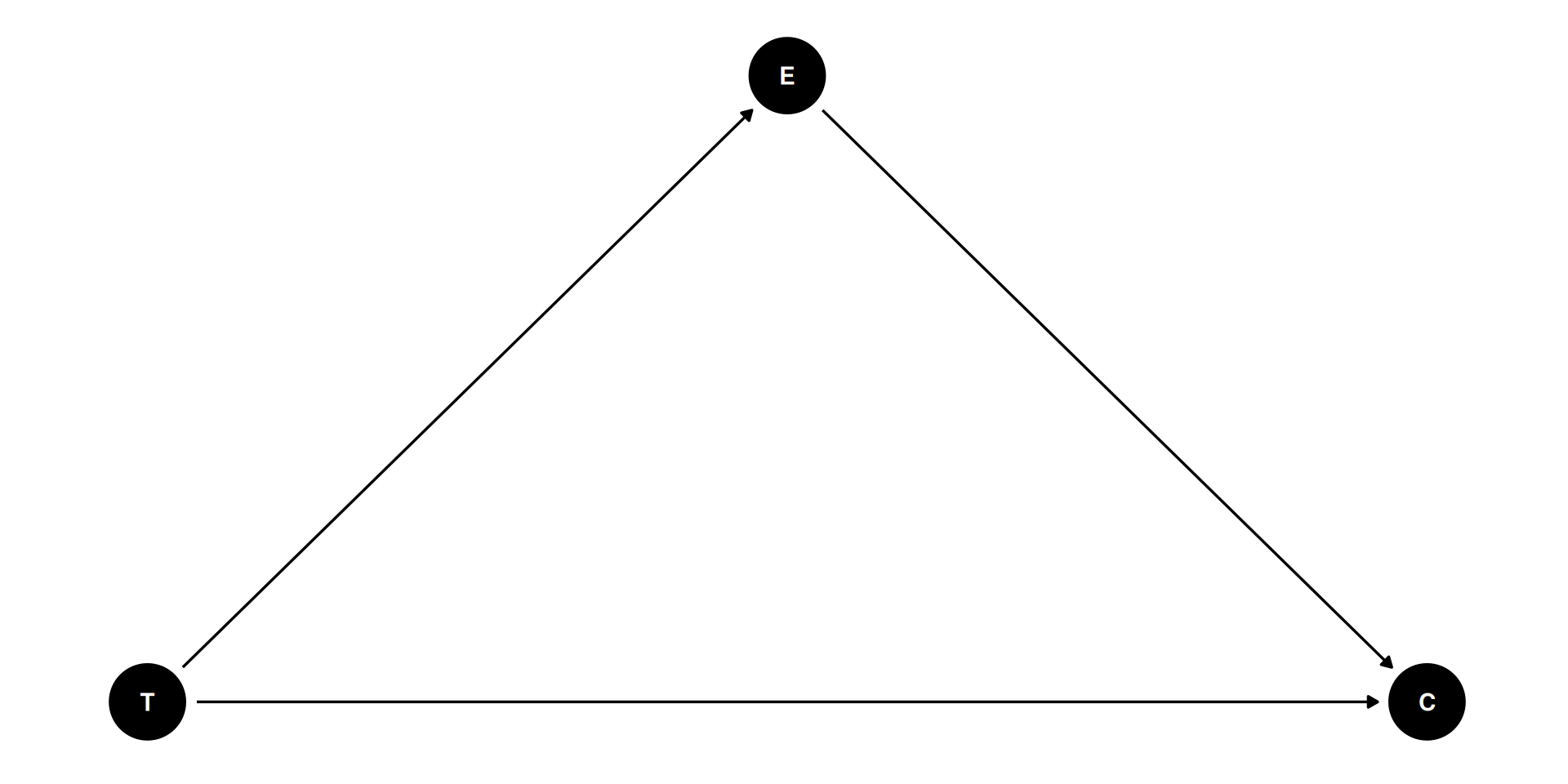
In the DAG, E is a post-treatment variable potentially influenced by T
- E is a potential mediator
Important
A mediator is very different from a confounder
Direct Effect
Causal effect when holding mediator at a specific level (e.g., T → C when E = 5)
Controlled direct effect
| tone | emo | Estimate | Est.Error | Q2.5 | Q97.5 |
|---|---|---|---|---|---|
| 0 | 0 | 0.121 | 0.032 | 0.066 | 0.191 |
| 1 | 0 | 0.108 | 0.033 | 0.054 | 0.183 |
| 0 | 9 | 0.698 | 0.070 | 0.556 | 0.823 |
| 1 | 9 | 0.670 | 0.063 | 0.542 | 0.786 |
Natural Direct Effect
Comparing two potential outcomes: (a) Y(T = 1, M = M[0]) and (b) Y(T = 0, M = M[0])
E.g., What would the effect of negatively-framed story be had it not elicited negative emotions?
Natural Indirect Effect
Change in \(Y\) of the control group if their mediator level changes to what the treatment group would have obtained
i.e., Y(T = 0, M = M[1]) - Y(T = 0, M = M[0])
E.g., What would the effect of negatively-framed story be had it only elicited negative emotions, but did not affect anything else?
Notes on Mediation
- When the effects of T → M (usually called the a path) and M → Y (usually called the b path) are assumed linear, the indirect effect equals the product of the paths (ab)
- When a and/or b are not linear, the indirect effect is not constant across different levels of T and M
- Also the case when there is interaction between the treatment and the mediator
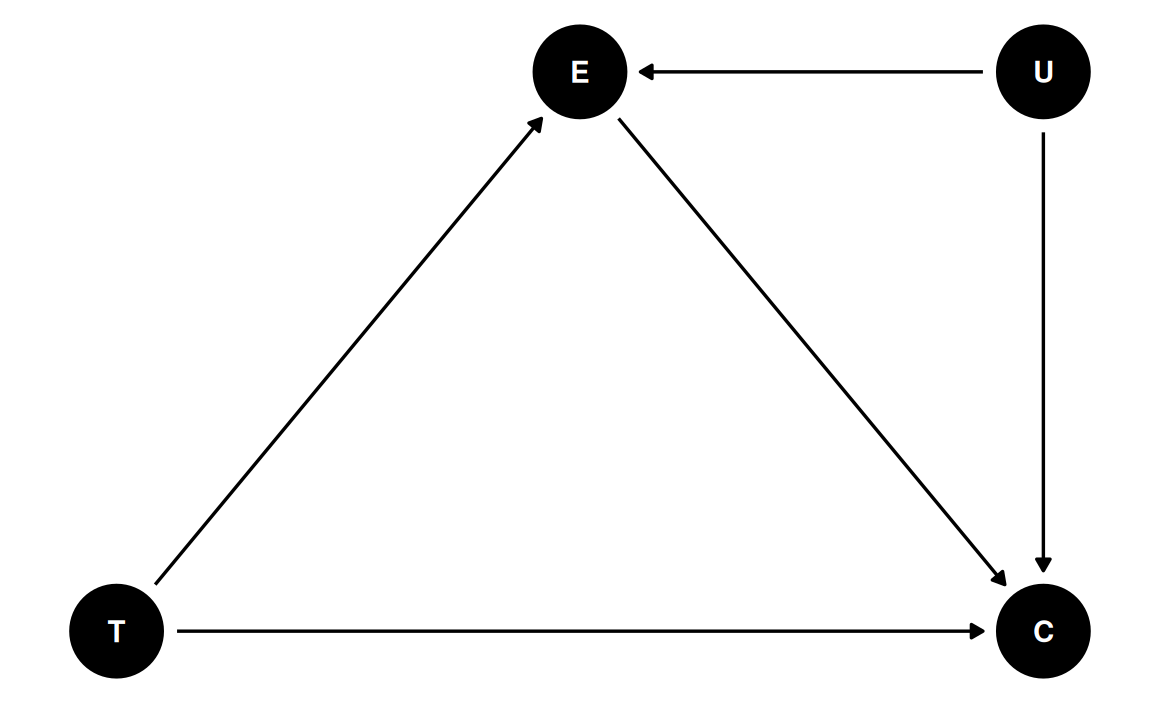
Assumptions of Mediation
- No unmeasured treatment-outcome confounding
- No unmeasured mediator-outcome confounding
- No unmeasured treatment-mediator confounding
- The mediator-outcome path is not moderated by the treatment
Note: randomization of the treatment only rules out confounding for T → M, but not for M → Y
Sensitivity Analysis
Assign priors representing plausible magnitude of confounding (see notes for an example)
Collider Bias
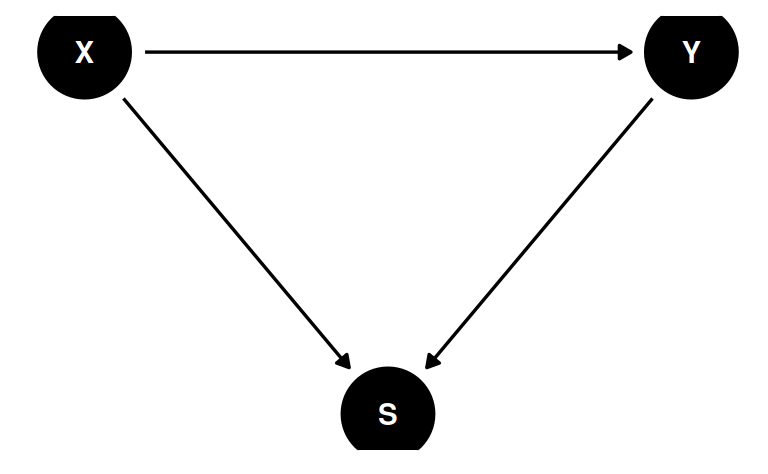
E.g., Is the most newsworthy research the least trustworthy?
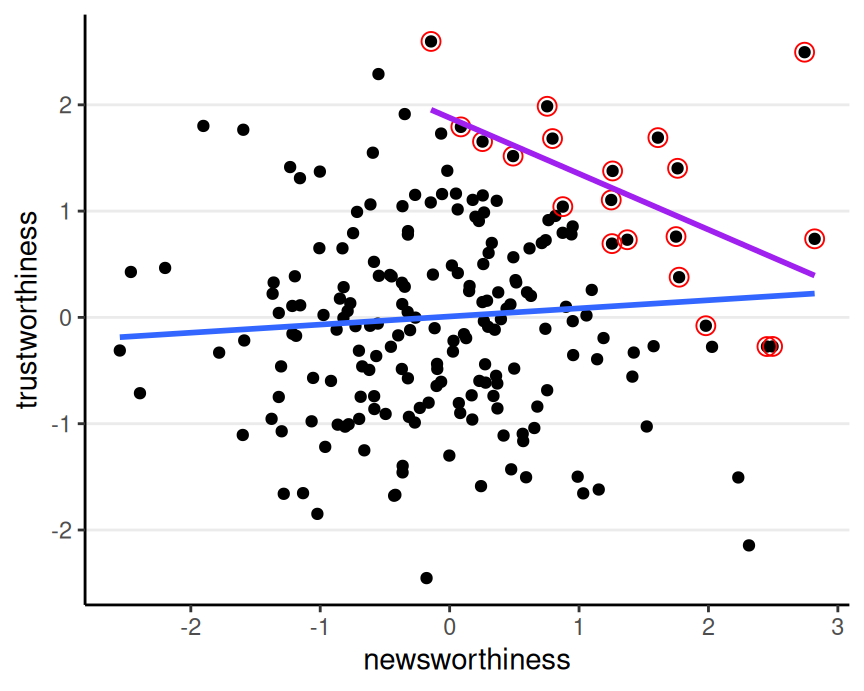
Collider Bias in Real Research/Real Life
- Adjusting for current neighborhood when estimating effect of schooling on earnings
- Studying the link between impulsivity and delinquency among high-risk youth
- Estimating association between standardized test among students admitted
- Studying infant mortality and maternal smoking among infants with low birth weight
Instrumental Variables
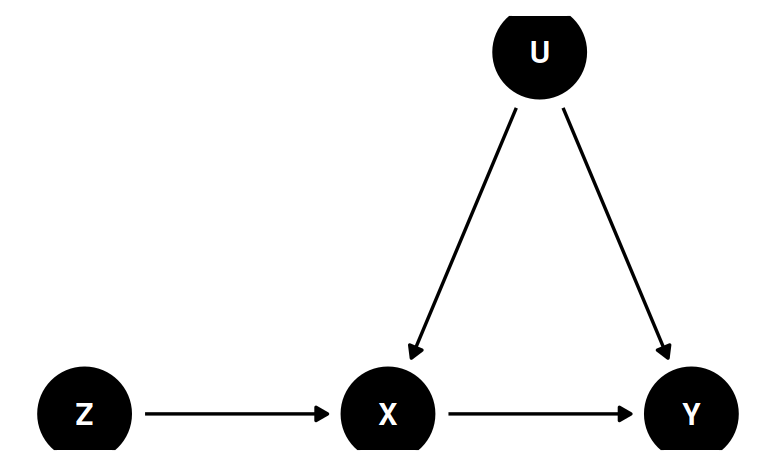
- X = Career Adaptability
- Y = Job Satisfaction
- Z (instrument) = Conscientiousness
- U = Confounding
Instrument
- Plausible cause of X
- Can only affect Y through X
Other Examples of Instrumental Variables
- Distance to the nearest college for the effect of education on earnings
- Hospital’s encouragement on the effect of breastfeeding on weight outcomes
Some Other Topics for Causal Inference
- Propensity score analysis
- Estimate probability of being in the treatment for each participant based on other covariates
- Balancing out pre-treatment covariates so that the comparison more resembles a randomized experiments
- Regression discontinuity
- E.g., Assigning to treatment only when pre-test score is below a cutoff
- Pre-test score becomes the only confounding variable to be adjusted for
Remarks
- Causal inference requires causal assumptions
- You need a DAG
- Blindly adjusting for covariates does not give better results
- post-treatment bias, collider bias, etc
- Think carefully about what causal quantity is of interest
- E.g., direct, indirect, total
- Causal inferences are possible with both experimental and non-experimental data