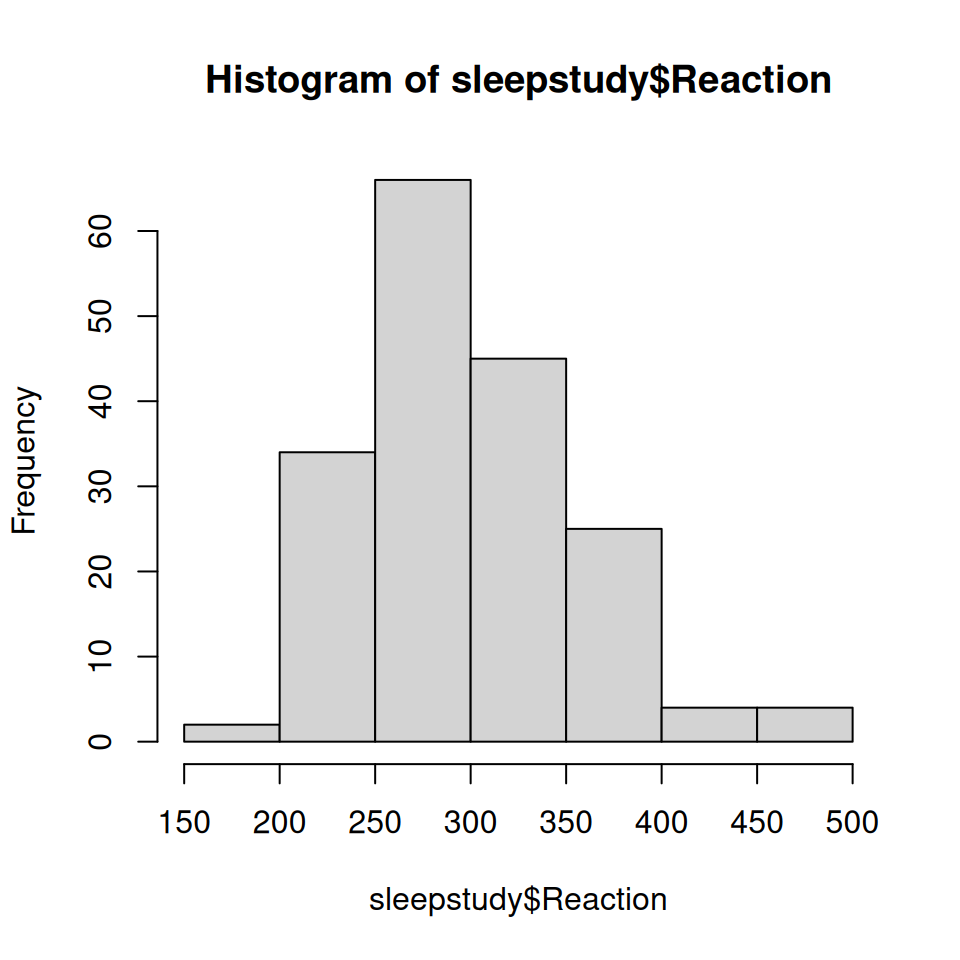
Reaction Days Subject
1 250 0 308
2 259 1 308
3 251 2 308
4 321 3 308
5 357 4 308
6 415 5 308Multilevel Models
PSYC 573
Guiding Questions
- What is hierarchical/multilevel models (MLMs)?
- How to fit Bayesian multilevel models?
- What are the advantages of MLM?
- How to allow separate regression lines for many groups/clusters?
- Varying intercepts and slopes (and variances)
- Interpretations
Multilevel Models
- Discovered in different disciplines separately
- Mixed/mixed-effect models
- Hierarchical linear models
- Variance component models
- A flexible class of models to handle clustered (dependent) data
- Extremely common in the behavioral and social sciences
MLM
MLM subsumes
- Dependent-sample \(t\)-test
- Random-effect ANOVA
- Repeated-measure ANOVA
- Variance components models
- Growth curve models
- Generalizability theory
- Random-effect meta-analysis
- Build cluster-specific regression/other types of models
- Borrow information across clusters
- Include higher-level predictors
Multilevel Data Structures
- Hierarchical/Nested
- Students in schools
- Clients nested within therapists within clinics
- Employees nested within organizations
- Citizens nested within employees
- Repeated measures nested within persons
Multilevel Data Structures (Cont’d)
- Crossed
- Students cross-classified by high schools and middle schools
- Responses cross-classified by items and persons
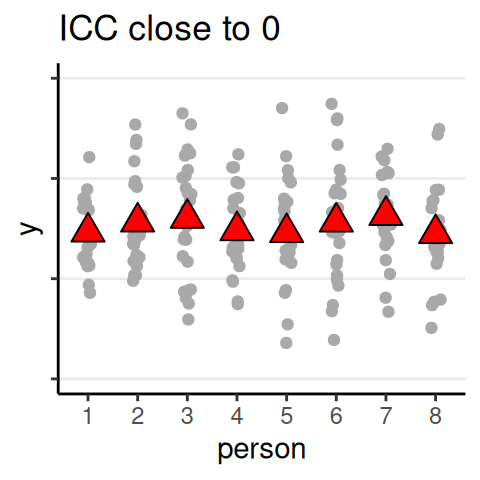
Quantifying Dependence
- Intraclass correlation (ICC): \(\rho = \dfrac{\tau^2}{\tau^2 + \sigma^2}\)
- Analogous to \(\eta^2\)/\(R^2\) effect size
ICC
The proportion of variance of the outcome that are due to between-level (e.g., between-group, between-person) differences
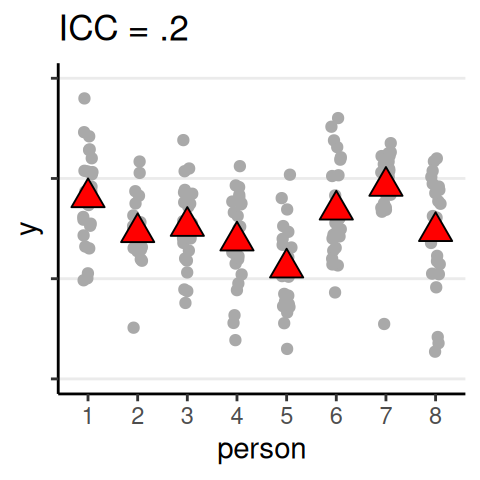
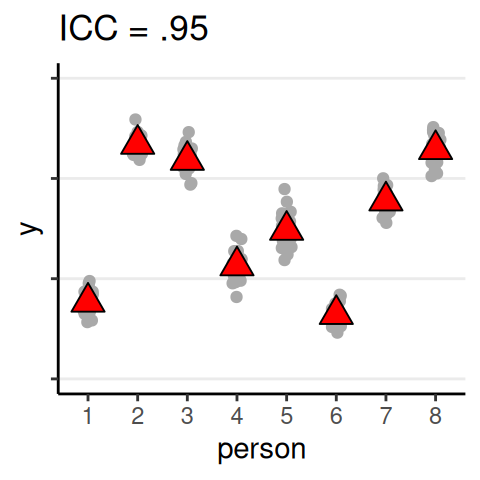
Data
Trajectories
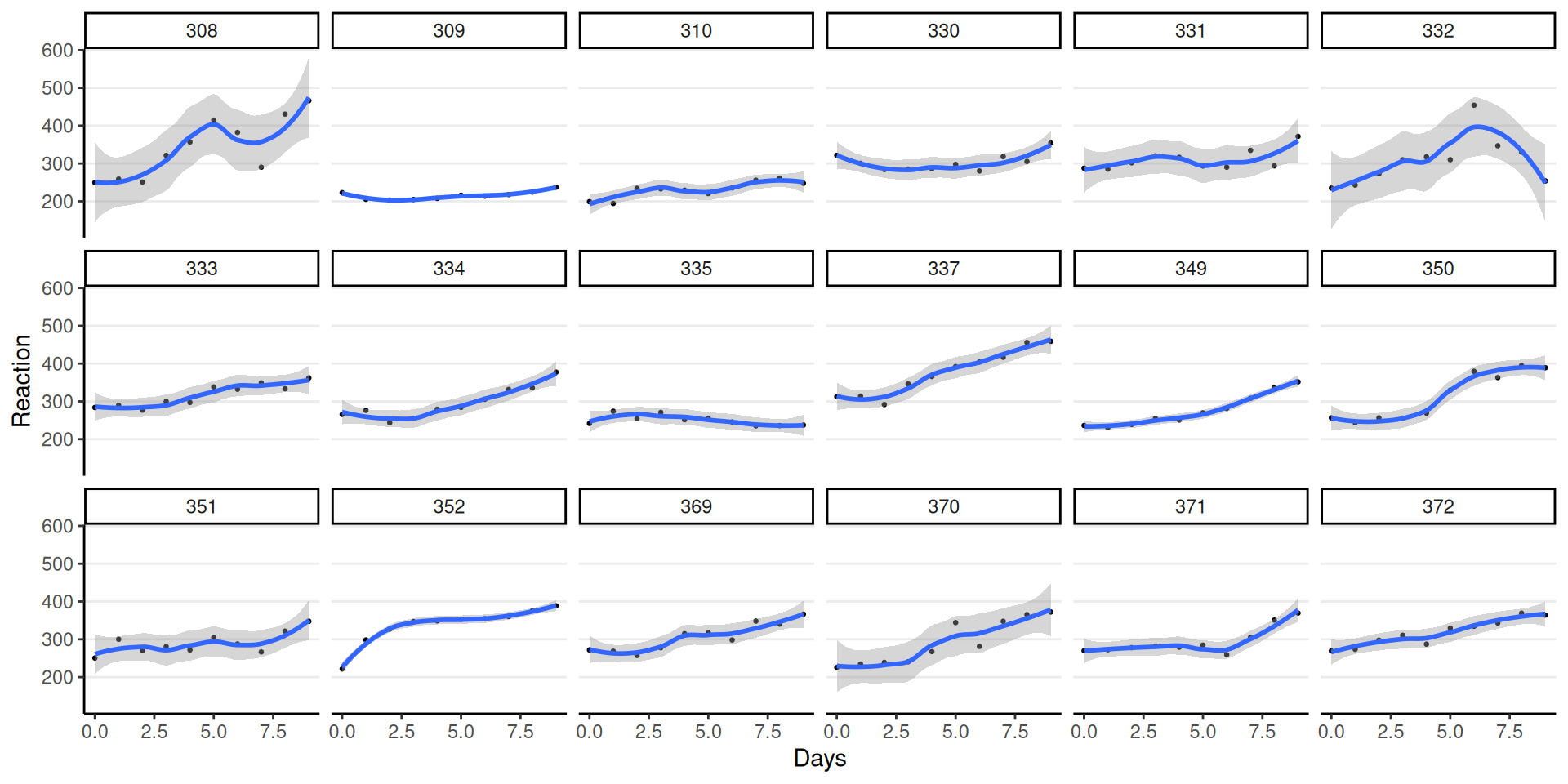
ICC of Reaction
- Varying/Random intercept model
\[ \begin{aligned} \text{Reaction}_{ij} & \sim N(\mu_j, \sigma) \\ \mu_j & \sim N(\gamma, \tau) \end{aligned} \]
- \(\mu_j\): mean reaction for the \(j\)th person
- \(i\) indexes measurement occasions
m2 <- brm(Reaction10 ~ (1 | Subject), data = sleepstudy,
prior = c(# for intercept
prior(normal(0, 50), class = "Intercept"),
# for tau
prior(gamma(2, 0.2), class = "sd"),
# for sigma
prior(student_t(4, 0, 5), class = "sigma")),
# Higher adapt_delta is usually needed for MLM
control = list(adapt_delta = .95),
seed = 2107,
file = "11_m2")| variable | median | mad | q5 | q95 |
|---|---|---|---|---|
| b_Intercept | 29.80 | 0.953 | 28.14 | 31.44 |
| sd_Subject__Intercept | 3.81 | 0.761 | 2.77 | 5.58 |
| sigma | 4.44 | 0.250 | 4.05 | 4.87 |
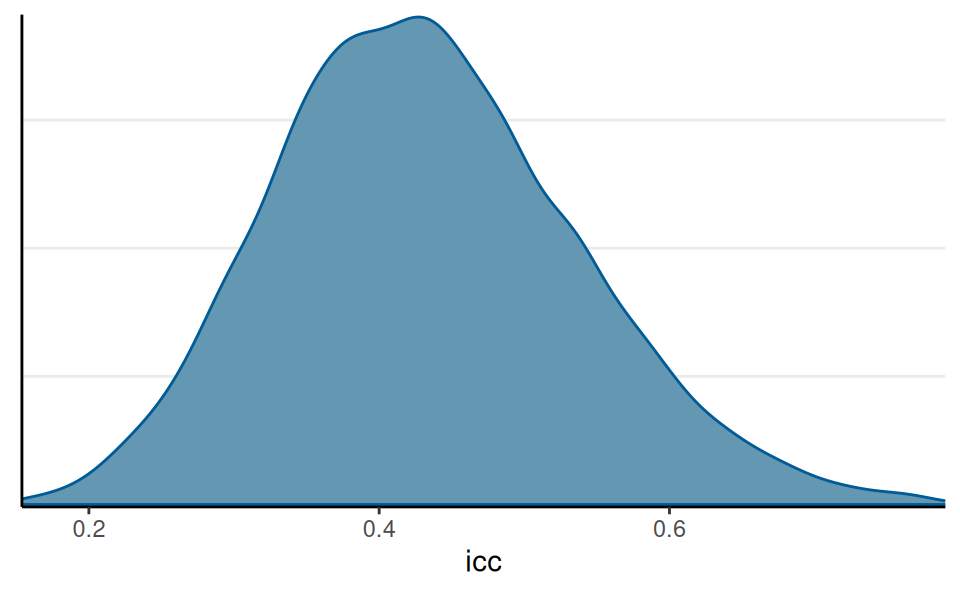
Interpretations
The model suggested that the average reaction time across individuals and measurement occasions was 298ms, 90% CI [281ms, 314ms]. It was estimated that 43.22%, 90% CI [27.12%, 61.31%] of the variations in reaction time was attributed to between-person differences.
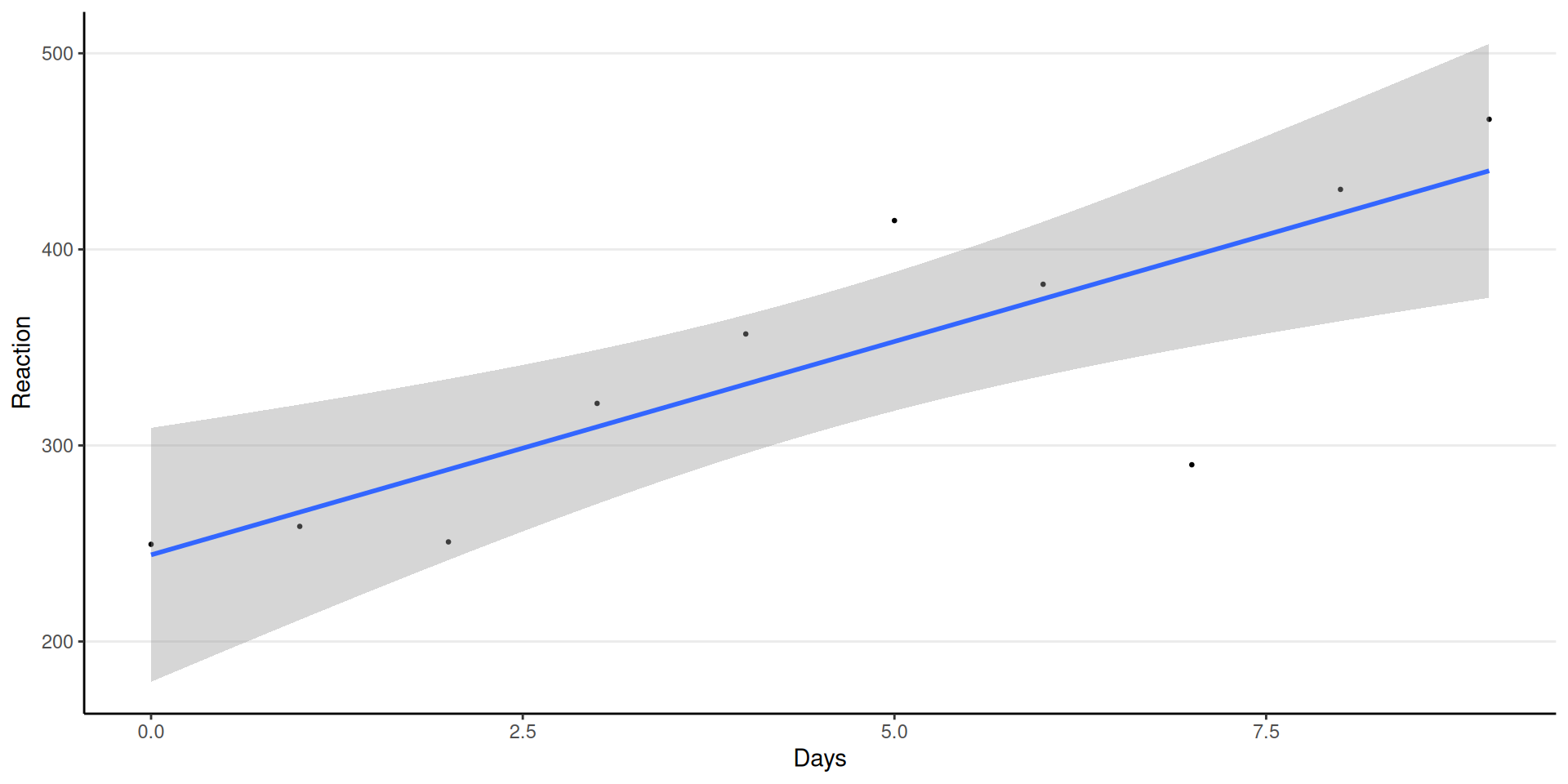
Regression for One Person (308)
\[ \begin{aligned} \text{Reaction10}_i & \sim N(\mu_i, \sigma) \\ \mu_i & = \beta_0 + \beta_1 \texttt{Days}_i \end{aligned} \]
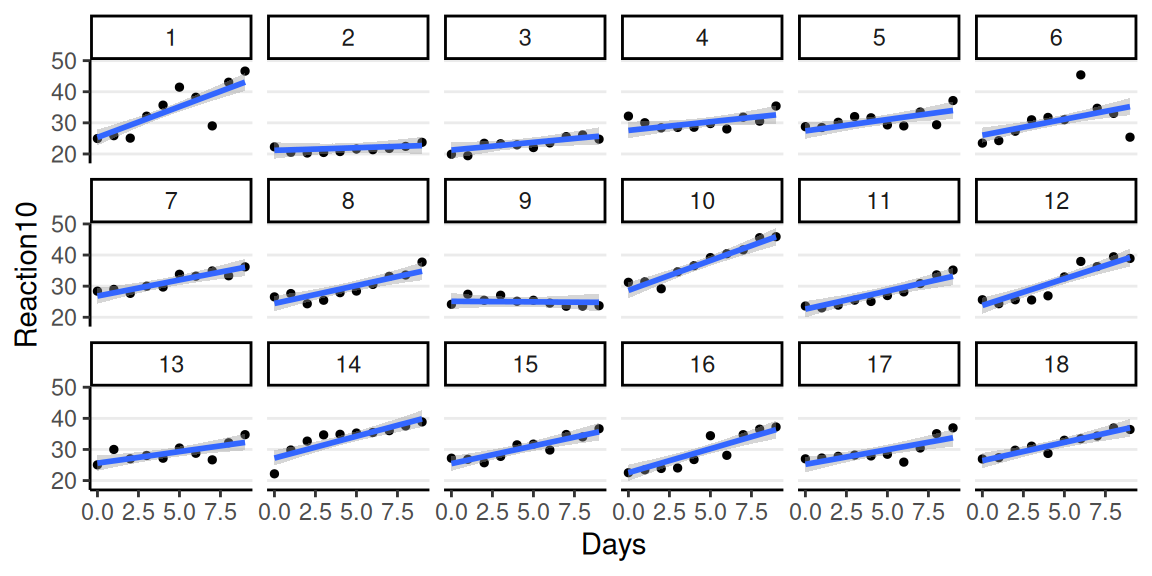
Varying Coefficients
In MLM, parameters (\(\beta_0\), \(\beta_1\), \(\sigma\)) can be
- different across clusters (persons)
- be estimated by partial pooling
Varying Intercepts
Repeated-measure level:
\[ \begin{aligned} \text{Reaction10}_{ij} & \sim N(\mu_{ij}, \sigma) \\ \mu_{ij} & = \beta_{0j} + \beta_{1} \text{Days}_{ij} \\ \end{aligned} \]
Person level:
\[ \begin{aligned} \beta_{0j} & \sim N(\mu^{[\beta_0]}, \tau^{[\beta_0]}) \\ \end{aligned} \]
Priors:
\[ \begin{aligned} \mu^{[\beta_0]} & \sim N(0, 50) \\ \tau^{[\beta_0]} & \sim \mathrm{Gamma}(2, 0.2) \\ \beta_1 & \sim N(0, 10) \\ \sigma & \sim t^+(4, 0, 5) \end{aligned} \]
m3 <- brm(Reaction10 ~ Days + (1 | Subject),
data = sleepstudy,
prior = c( # for intercept
prior(normal(0, 50), class = "Intercept"),
# for slope
prior(normal(0, 10), class = "b"),
# for tau
prior(gamma(2, 0.2), class = "sd"),
# for sigma
prior(student_t(4, 0, 5), class = "sigma")
),
control = list(adapt_delta = .95),
seed = 2107,
file = "11_m3"
)| variable | median | mad | q5 | q95 |
|---|---|---|---|---|
| b_Intercept | 25.23 | 1.054 | 23.552 | 26.93 |
| b_Days | 1.05 | 0.081 | 0.915 | 1.18 |
| sd_Subject__Intercept | 3.98 | 0.745 | 2.972 | 5.64 |
| sigma | 3.11 | 0.166 | 2.855 | 3.42 |
Overall Fit
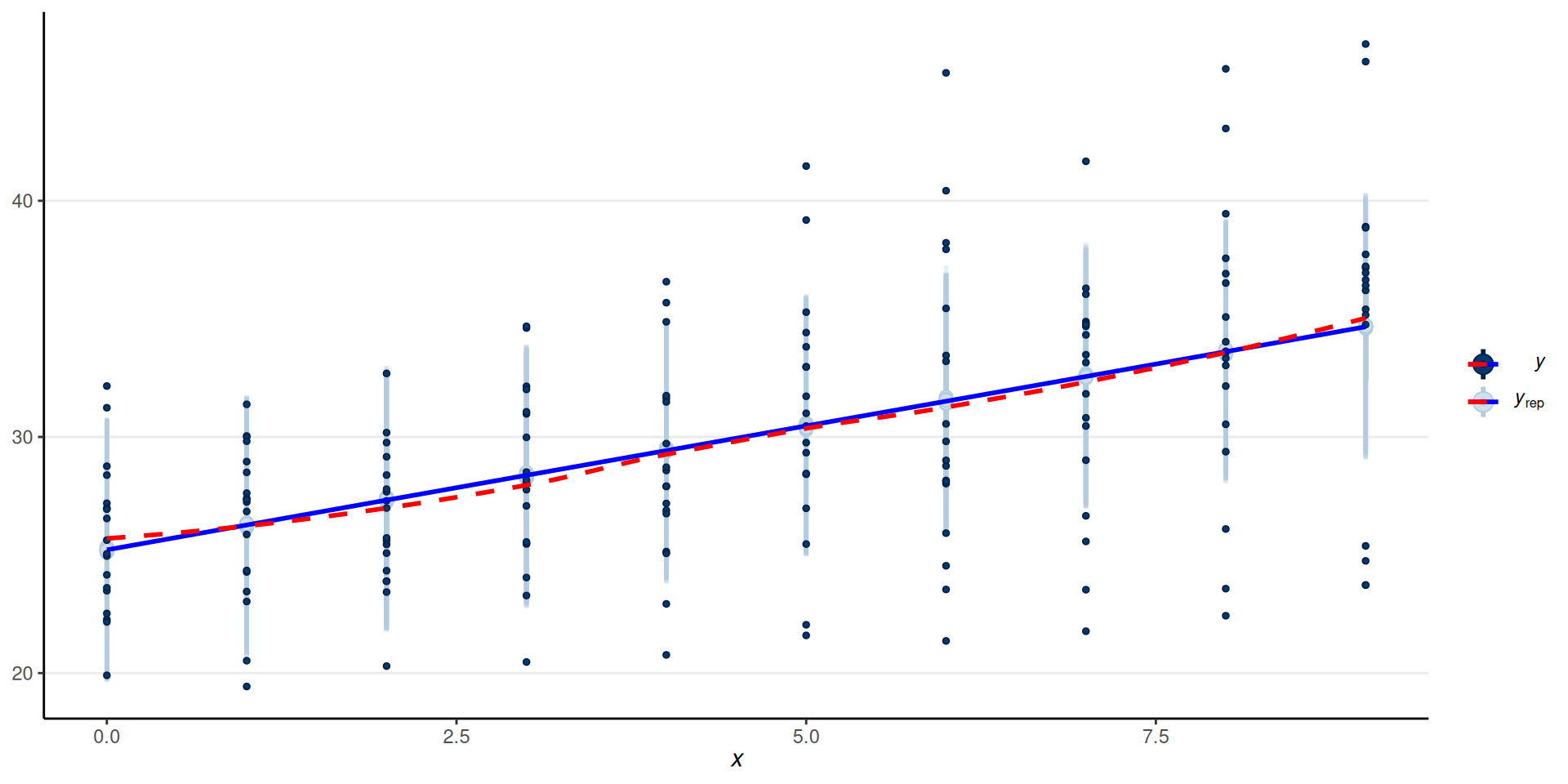
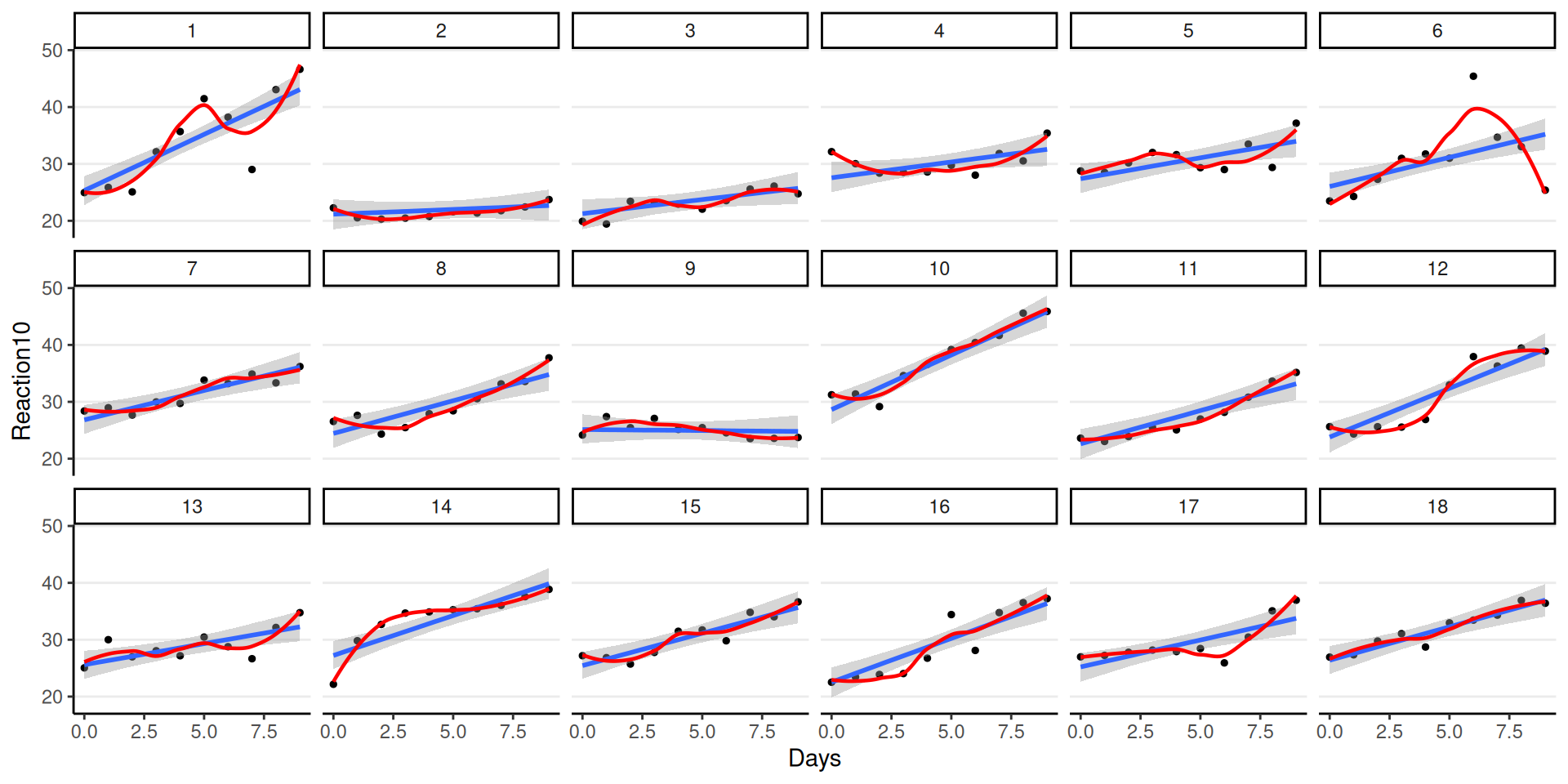
Fit to Individuals
Remember: The model assumes equal slopes for each person
Varying Slopes
Repeated-measure level:
\[ \begin{aligned} \text{Reaction10}_{ij} & \sim N(\mu_{ij}, \sigma) \\ \mu_{ij} & = \beta_{0j} + \beta_{1j} \text{Days}_{ij} \\ \end{aligned} \]
Person level:
\[ \begin{aligned} \begin{bmatrix} \beta_{0j} \\ \beta_{1j} \\ \end{bmatrix} & \sim N_2\left( \begin{bmatrix} \mu^{[\beta_0]} \\ \mu^{[\beta_1]} \\ \end{bmatrix}, \mathbf T \right) \\ \mathbf T & = \begin{bmatrix} {\tau^{[\beta_0]}}^2 & \\ \tau^{\beta{10}} & {\tau^{[\beta_1]}}^2 \\ \end{bmatrix} \end{aligned} \]
LKJ Prior
Decomposing Covariance Matrix
- Covariance = SD \(\times\) Correlation \(\times\) SD
\[ \mathbf T = \mathrm{diag}(\boldsymbol{\tau}) \boldsymbol{\Omega} \mathrm{diag}(\boldsymbol{\tau}) \]
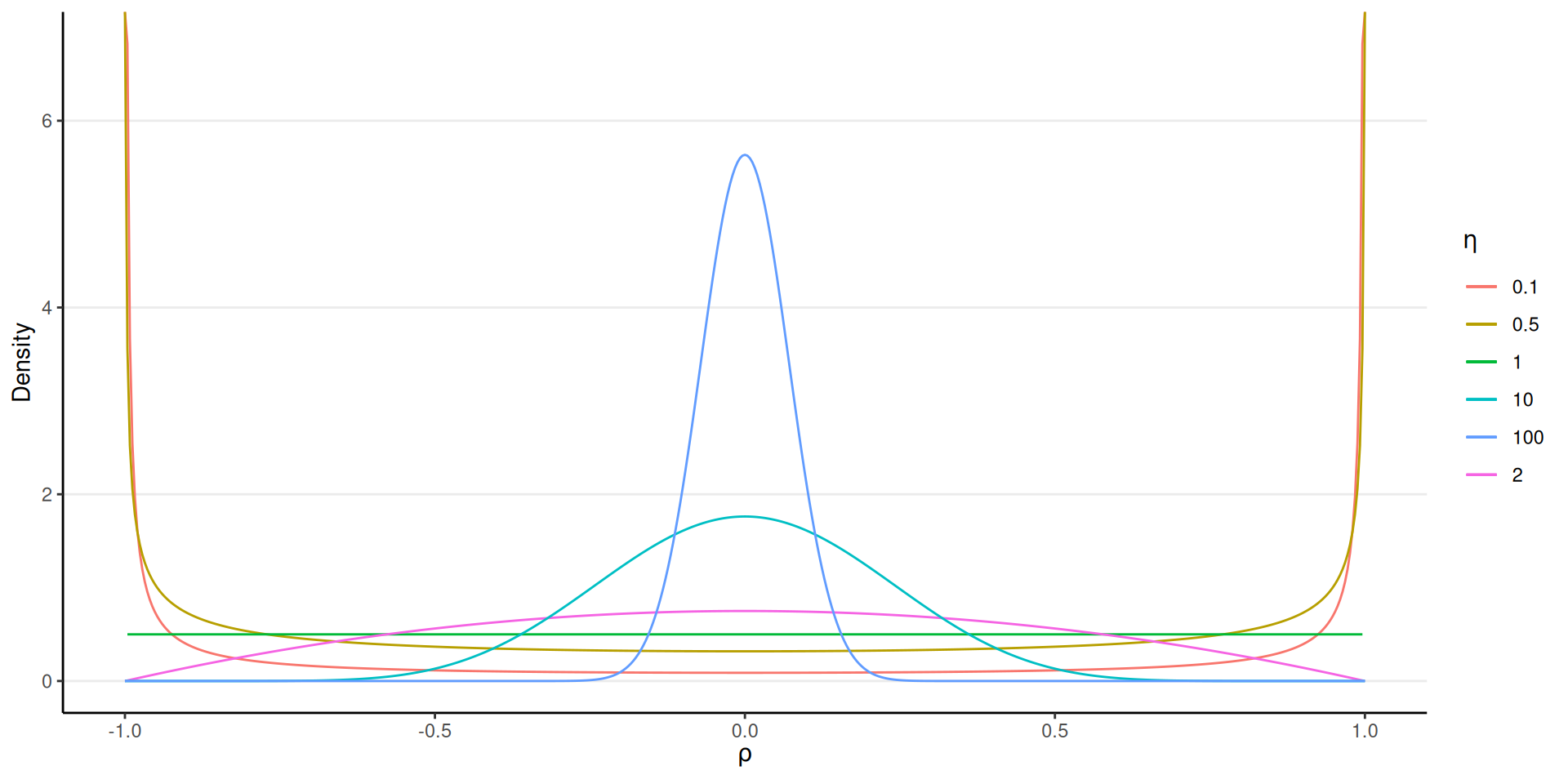
Shape parameter \(\eta\)
\[ P(\boldsymbol{\Omega} | \eta) \propto \det(\boldsymbol{\Omega})^{\eta - 1} \]
- \(\eta = 1\): Uniform
- \(\eta \geq 1\): increasingly concentrated to zero correlations
- \(\eta \leq 1\): more correlations closer to 1
Priors
\[ \begin{aligned} \mu^{[\beta_0]} & \sim N(0, 50) \\ \mu^{[\beta_1]} & \sim N(0, 10) \\ \tau^{[\beta_m]} & \sim \mathrm{Gamma}(2, 0.2), \; m = 0, 1 \\ \boldsymbol{\Omega} & \sim \mathrm{LKJ}(1) \\ \sigma & \sim t^+(4, 0, 5) \end{aligned} \]
m4 <- brm(Reaction10 ~ Days + (Days | Subject),
data = sleepstudy,
prior = c( # for intercept
prior(normal(0, 50), class = "Intercept"),
# for slope
prior(normal(0, 10), class = "b"),
# for tau_beta0 and tau_beta1
prior(gamma(2, 0.2), class = "sd", group = "Subject"),
# for correlation
prior(lkj(1), class = "cor"),
# for sigma
prior(student_t(4, 0, 5), class = "sigma")
),
control = list(adapt_delta = .95),
seed = 2107,
file = "11_m4"
)| variable | median | mad | q5 | q95 |
|---|---|---|---|---|
| b_Intercept | 25.122 | 0.731 | 23.835 | 26.39 |
| b_Days | 1.036 | 0.167 | 0.765 | 1.34 |
| sd_Subject__Intercept | 2.755 | 0.671 | 1.806 | 4.09 |
| sd_Subject__Days | 0.666 | 0.146 | 0.468 | 1.00 |
| cor_Subject__Intercept__Days | 0.058 | 0.327 | -0.450 | 0.58 |
| sigma | 2.582 | 0.157 | 2.339 | 2.87 |
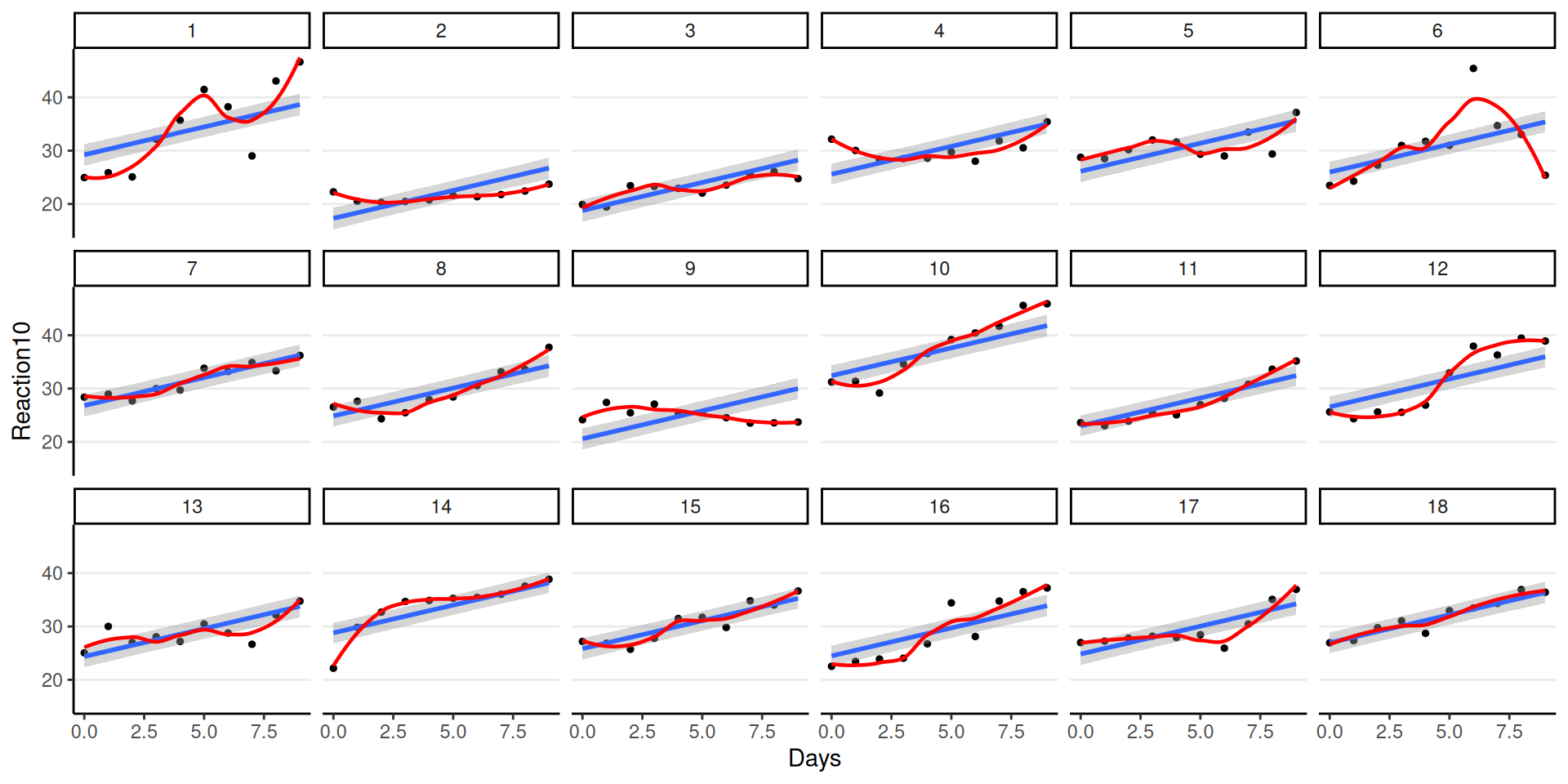
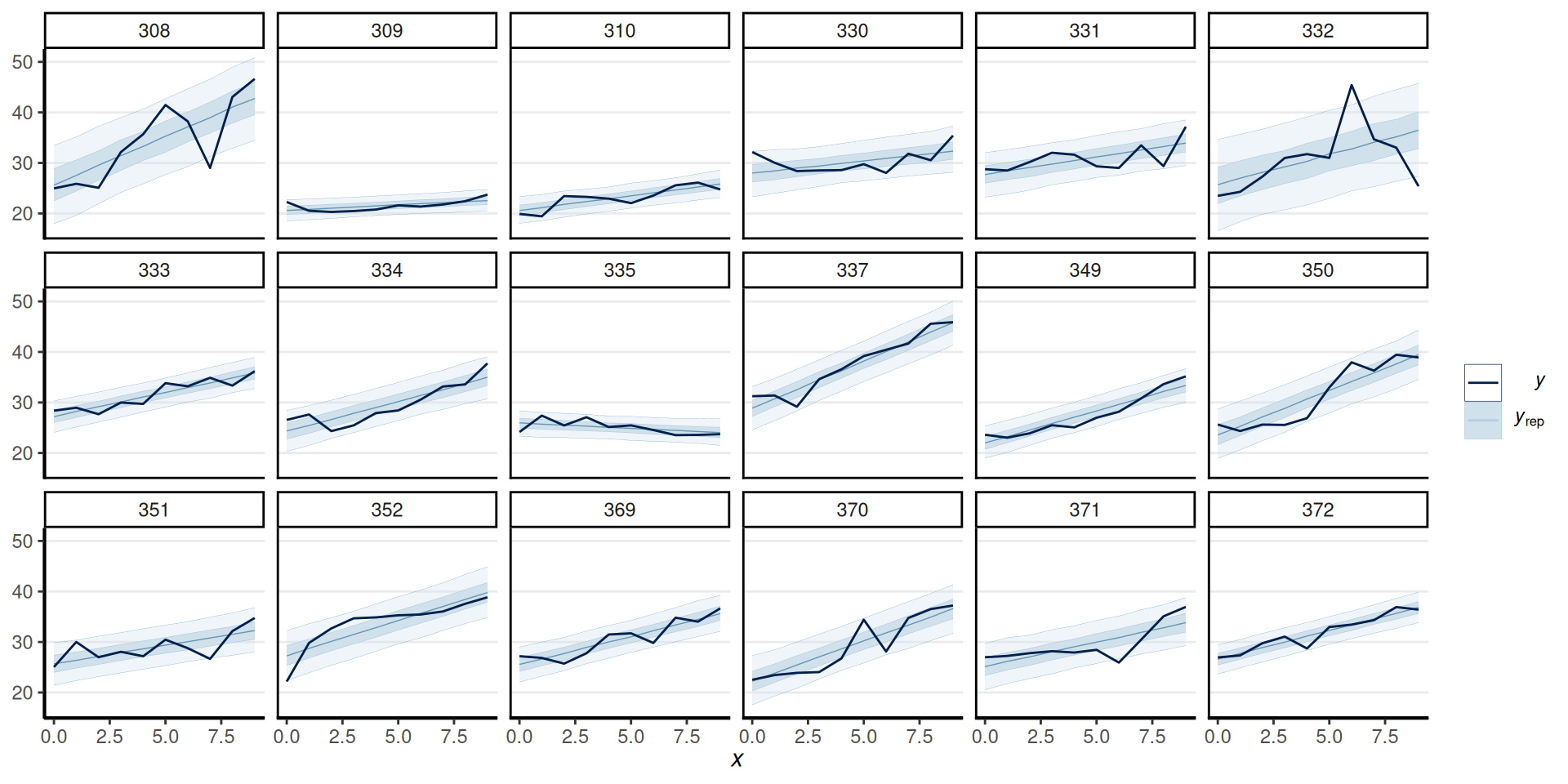
Fit to Individuals
Varying Regression Lines
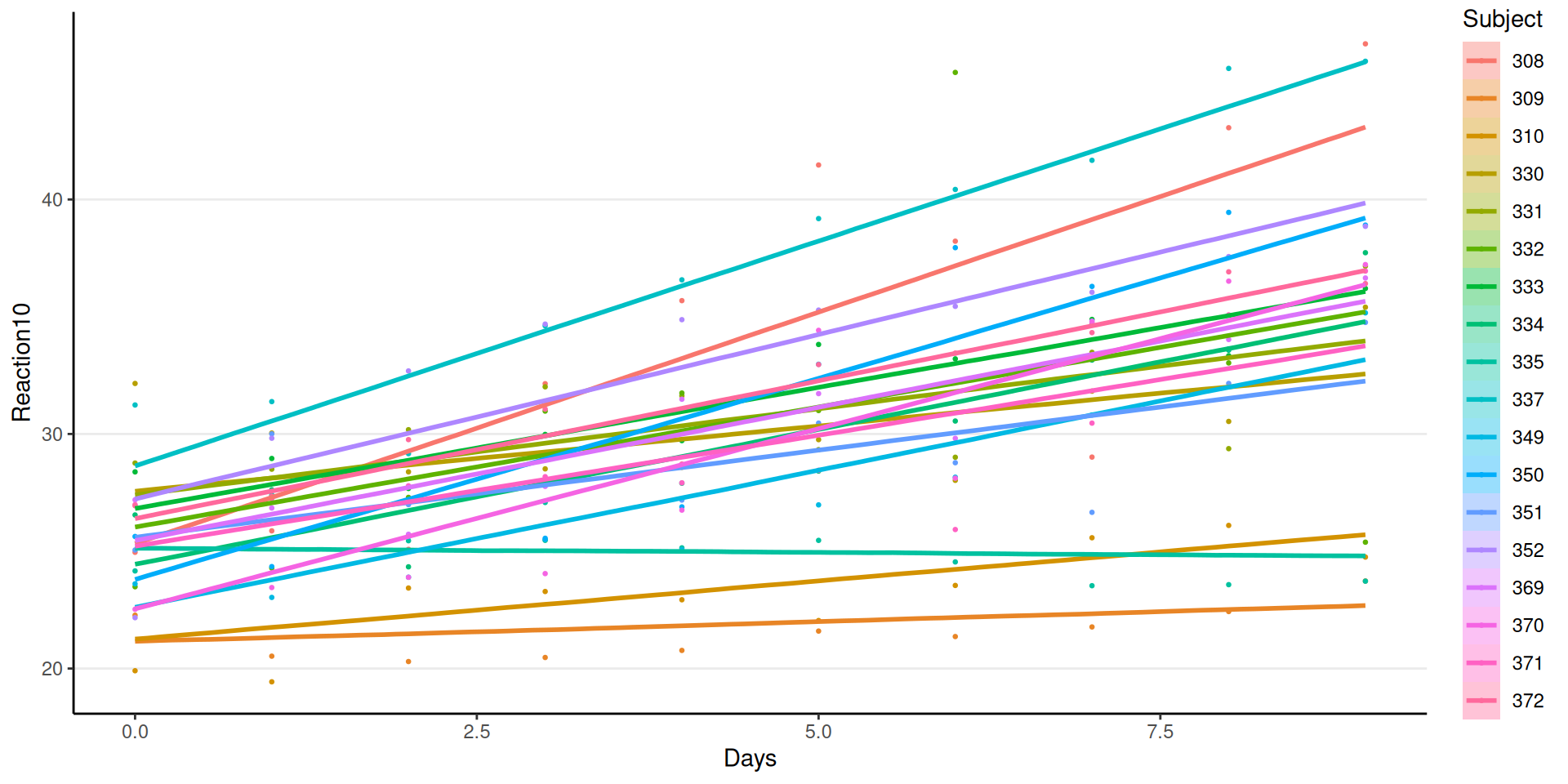
Interpretations
\(\beta_0\)
Based on the model, at Day 0, the average reaction time across individuals was 251ms, 90% CI [238ms, 264ms], and the SD at Day 0 was 28.318ms, 95% CI [18.061ms, 40.863ms].
\(\beta_1\)
The average rate of change per day in reaction time across individuals was 10ms, 90% CI [7.6ms, 13ms], and the SD of the rates of change at Day 0 was 6.901ms, 95% CI [4.681ms, 10.049ms].
Random \(\sigma\)
Comparing Models
| effect | Var Int | Var Slp | Var \(\sigma\) | |
|---|---|---|---|---|
| fixed | \(\mu^{[\beta_0]}\) | 25.23 [23.16, 27.27] | 25.12 [23.55, 26.66] | 25.11 [23.52, 26.77] |
| \(\mu^{[\beta_1]}\) | 1.05 [0.89, 1.21] | 1.04 [0.70, 1.41] | 1.04 [0.70, 1.40] | |
| \(\sigma\) | 3.11 [2.81, 3.49] | 2.58 [2.29, 2.92] | ||
| \(\mu^{[\log \sigma]}\) | 0.73 [0.44, 1.02] | |||
| random | \(\tau^{[\beta_0]}\) | 3.98 [2.85, 6.04] | 2.75 [1.68, 4.41] | 3.06 [2.06, 4.87] |
| \(\tau^{[\beta_1]}\) | 0.67 [0.44, 1.09] | 0.68 [0.46, 1.07] | ||
| \(\tau^{[\log \sigma]}\) | 0.49 [0.31, 0.79] | |||
| Num.Obs. | 180 | 180 | 180 | |
| ELPD | −470.0 | −447.0 | −418.5 | |
| ELPD s.e. | 14.3 | 22.7 | 13.4 | |
| LOOIC | 940.0 | 894.0 | 837.0 | |
| LOOIC s.e. | 28.6 | 45.5 | 26.8 | |
| WAIC | 939.5 | 891.0 | 827.6 |
Many More Topics in MLM
- Adding higher-level predictors
- Cross-level interactions
- Decomposing effects and the ecological fallacy
- Categorical outcomes (i.e., generalized linear mixed model, GLMM)
- Complex data structures (e.g., 3-level, crossed)
- And more . . . Check out MLM classes on campus