Model Comparison

PSYC 573

Guiding Questions

  • What is overfitting and why is it problematic?
  • How to measure closeness of a model to the true model?
    • What do information criteria do?

In-Sample and Out-Of-Sample Prediction

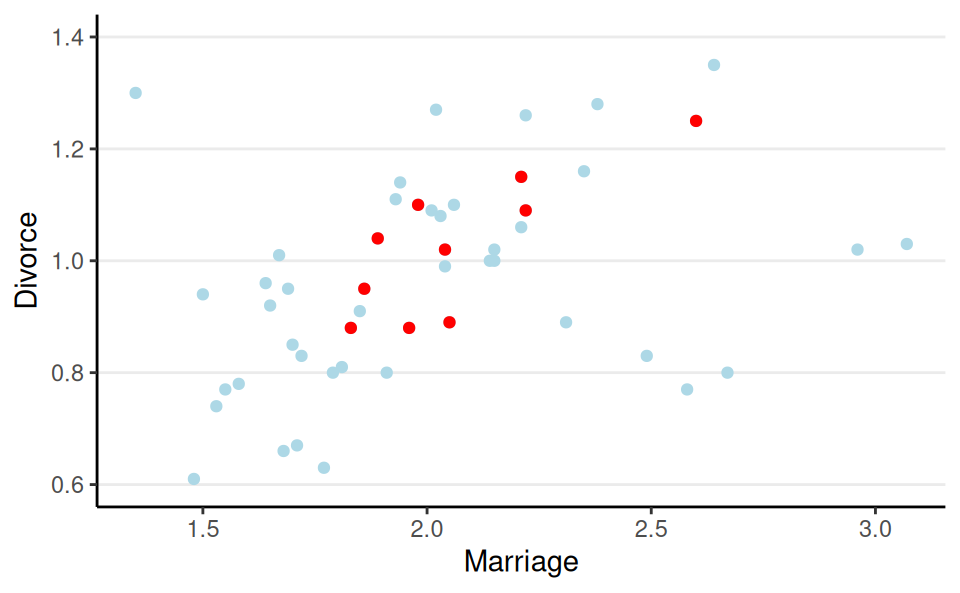
  • Randomly sample 10 states

Underfitting and Overfitting

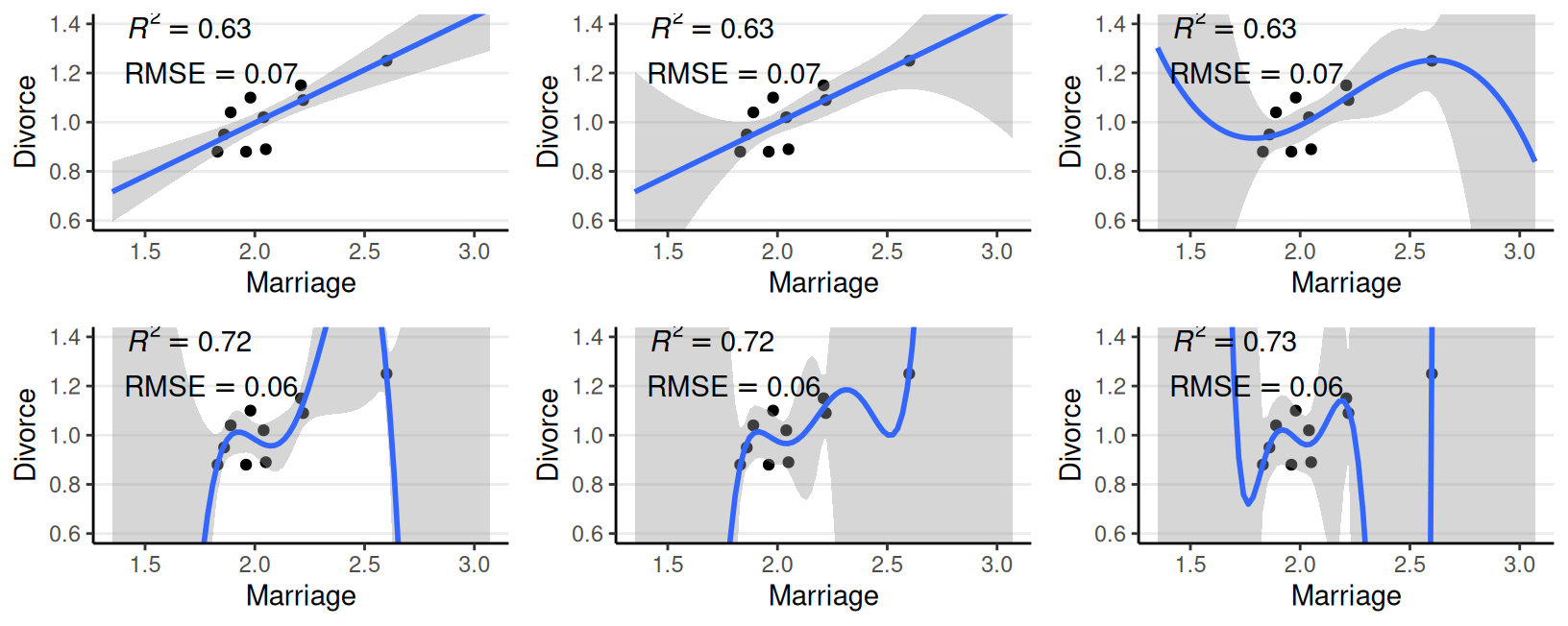
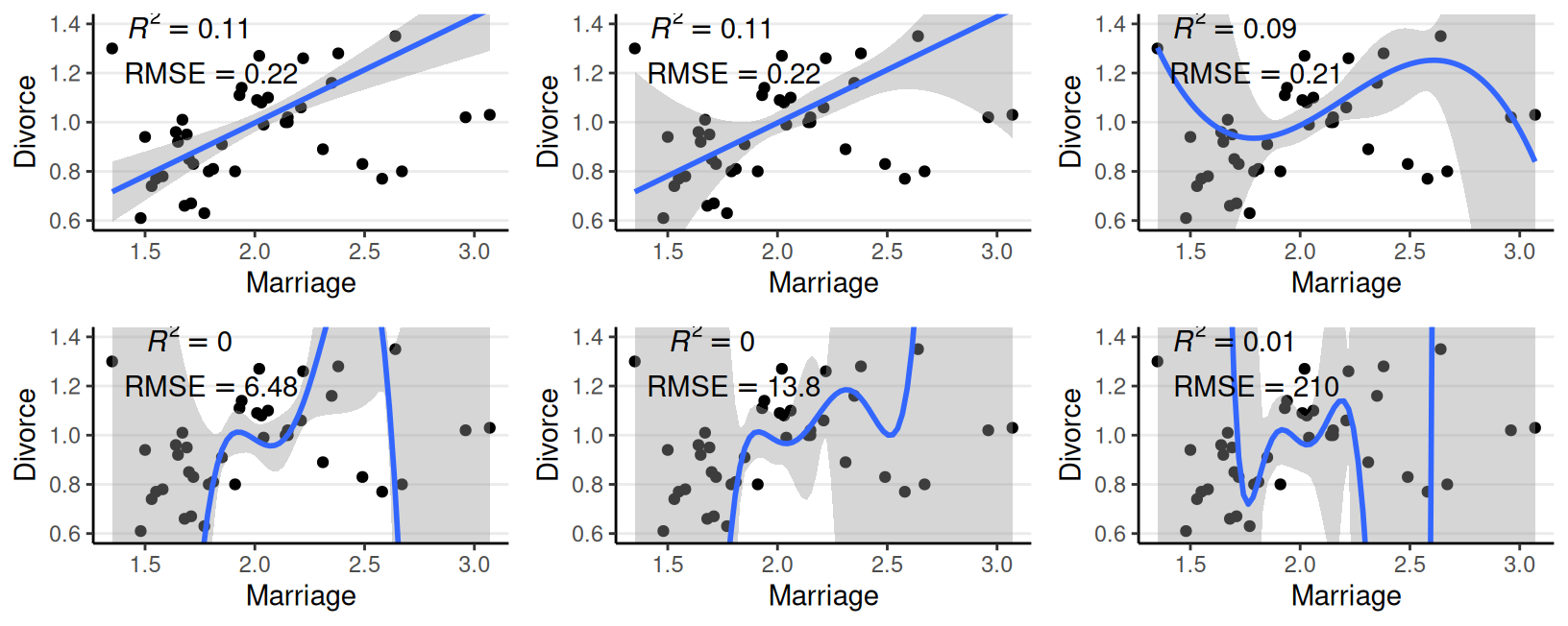
Complex models require more data

  • Too few data for a complex model: overfitting
  • A model being too simple: underfitting

Prediction of Future Observations

  • The more a model captures the noise in the original data, the less likely it predicts future observations well

Terminologies

What it is (roughly) Better when index is
Entropy Amount of uncertainty/information in the outcome variable(s) —
KL Divergence “Discrepancy” from “true” model smaller
elpd “Fit” to sample data larger
deviance \(-2\) \(\times\) in-sample elpd smaller
AIC/WAIC out-of-sample prediction error smaller
LOOIC out-of-sample prediction error smaller

What Is A Good Model?

  • Closeness from the proposed model (\(M_1\)) to a “true” model (\(M_0\))
    • Kullback-Leibler Divergence (\(D_\textrm{KL}\))
      = \(\text{Entropy of }M_0 - \text{elpd of }M_1\)
    • elpd: expected log predictive density: \(E_{M_0}[\log P_{M_1}(\tilde {\mathbf{y}})]\)
  • Choose a model with smallest \(D_\textrm{KL}\)
    • When \(M_0 = M_1\), \(D_\textrm{KL} = 0\)
    • \(\Rightarrow\) choose a model with largest elpd

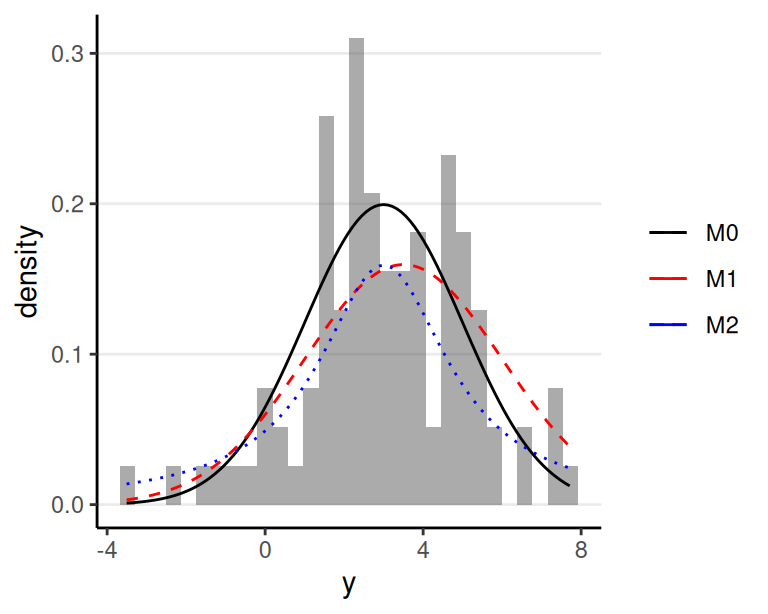
Example

  • True model of data: \(M_0\): \(y \sim N(3, 2)\)
  • \(M_1\): \(y \sim N(3.5, 2.5)\)
  • \(M_2\): \(y \sim \mathrm{Cauchy}(3, 2)\)

Entropy of \(M_0\) = -2.112

elpd \(D_\textrm{KL}(M_0 \mid M_.)\)
\(M_1\) -2.175 0.063
\(M_2\) -2.371 0.259

Expected log pointwise predictive density

\[ \sum_i \log P_{M_1} (y_i) \]

Note: elpd is a function of sample size

  • Problem: elpd depends on \(M_0\), which is unknown
    • Estimate elpd using the current sample \(\rightarrow\) underestimate discrepancy
    • Need to estimate elpd using an independent sample

Overfitting

Training set: 25 states; Test set: 25 remaining states

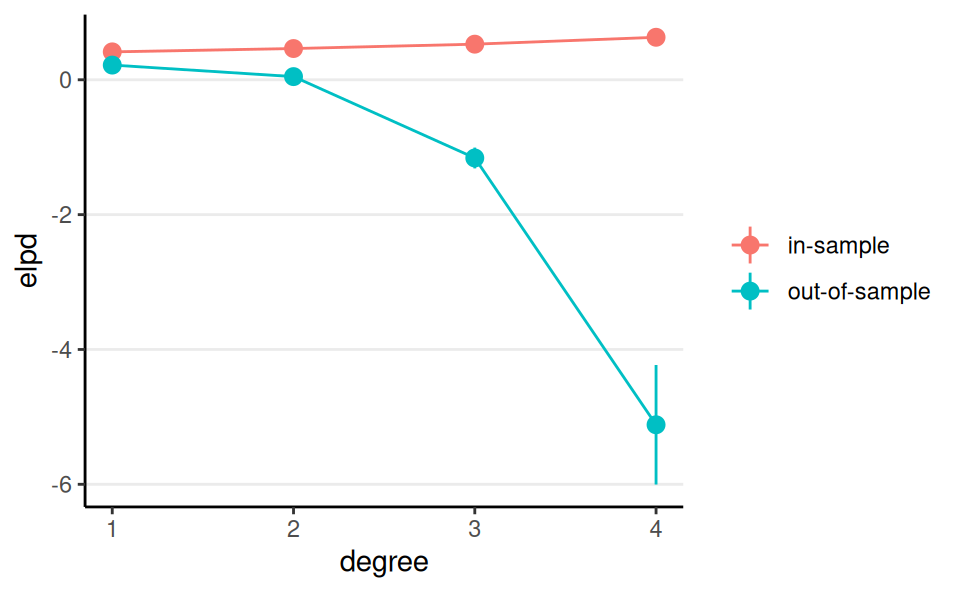
  • More complex model = more discrepancy between in-sample and out-of-sample elpd

Information Criteria (IC)

Approximate discrepancy between in-sample and out-of-sample elpd

  • IC = \(-2\) \(\times\) (in-sample elpd \(-\) \(p\))

  • \(p\) = penalty for model complexity

    • function of number of parameters

Choose a model with smaller IC

Bayesian ICs: DIC, WAIC, etc

Cross-Validation

  • Split the sample into K parts

  • Fit a model with K - 1 parts, and obtain elpd for the “hold-out” part

Leave-one-out: K = N

  • Very computationally intensive

  • loo package: approximation using Pareto smoothed importance sampling

loo(m1)

Computed from 8000 by 50 log-likelihood matrix.

         Estimate  SE
elpd_loo     15.0 5.0
p_loo         3.4 1.0
looic       -30.1 9.9
------
MCSE of elpd_loo is 0.0.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.7, 1.0]).

All Pareto k estimates are good (k < 0.7).
See help('pareto-k-diagnostic') for details.

Comparing Models

\[ \texttt{Divorce}_i \sim N(\mu_i, \sigma) \]

  • M1: Marriage
  • M2: Marriage, South, Marriage \(\times\) South
  • M3: South, smoothing spline of Marriage by South
  • M4: Marriage, South, MedianAgeMarriage, Marriage \(\times\) South, Marriage \(\times\) MedianAgeMarriage, South \(\times\) MedianAgeMarriage, Marriage \(\times\) South \(\times\) MedianAgeMarriage

M1  M2  M3  M4
b_Intercept 0.61 0.67 0.94 5.52
b_Marriage 0.18 0.13 −1.20
b_Southsouth −0.63 0.10 0.31
b_Marriage × Southsouth 0.37 0.54
bs_sMarriage × SouthnonMsouth_1 −0.47
bs_sMarriage × Southsouth_1 1.21
sds_sMarriageSouthnonMsouth_1 0.87
sds_sMarriageSouthsouth_1 0.50
b_MedianAgeMarriage −1.72
b_Marriage × MedianAgeMarriage 0.45
b_MedianAgeMarriage × Southsouth −0.34
b_Marriage × MedianAgeMarriage × Southsouth −0.09
ELPD 15.0 18.2 17.7 23.5
ELPD s.e. 5.0 5.5 5.9 6.2
LOOIC −30.1 −36.5 −35.3 −47.1
LOOIC s.e. 9.9 11.0 11.7 12.3
RMSE 0.17 0.15 0.14 0.13

Notes for Using ICs

  • Same outcome variable and transformation
  • Same sample size
    • Sample size could change when adding a predictor that has missing values
  • Cannot compare discrete and continuous models
    • E.g., Poisson vs. normal

Other Techniques

See notes on stacking and regularization

  • Stacking: average predictions from multiple models
  • Regularization: using sparsity-inducing priors to identify major predictors
  • Variable selection: using projection-based methods