| state | sex | diag | death | status | T.categ | age |
|---|---|---|---|---|---|---|
| VIC | M | 1991-03-05 | 1991-07-01 | A | hs | 36 |
| NSW | M | 1987-08-30 | 1988-03-11 | D | hs | 25 |
| QLD | M | 1989-10-09 | 1990-08-22 | D | hs | 36 |
| NSW | M | 1991-03-17 | 1991-07-01 | A | hs | 42 |
| NSW | M | 1986-04-12 | 1989-01-31 | D | hs | 40 |
| NSW | M | 1986-09-29 | 1987-03-25 | D | hs | 69 |
| NSW | M | 1989-08-24 | 1991-07-01 | A | hs | 37 |
| Other | F | 1988-10-19 | 1991-07-01 | A | id | 30 |
| NSW | M | 1990-04-07 | 1991-01-21 | D | hs | 30 |
| NSW | M | 1988-04-28 | 1990-04-07 | D | hs | 41 |
One Parameter Models
PSYC 573
2024-09-10
Bernoulli Model
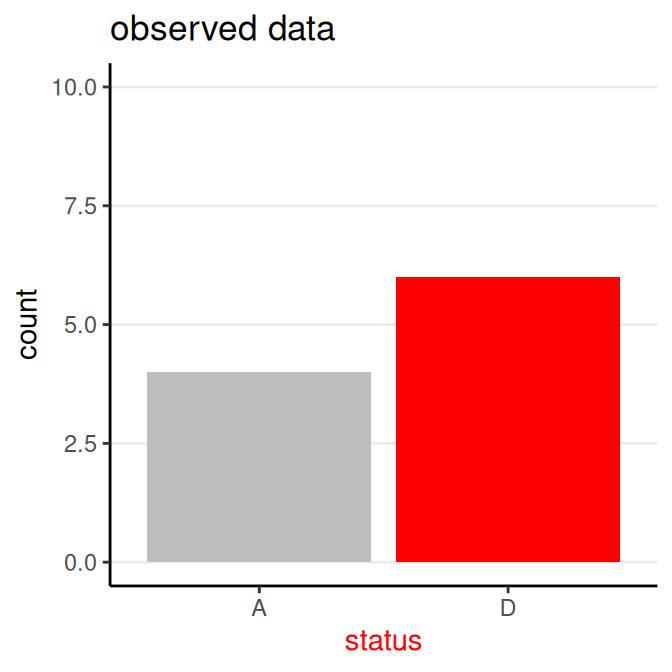
Data (Subsample)
- Patients diagnosed with AIDS in Australia before 1 July 1991

Let’s go through the Bayesian workflow
flowchart LR
subgraph DATA
direction TB
A[Identify/Collect Data] --> B[Visualize Data]
end
%% B --> C[Choose/Modify Model]
subgraph MODEL
H -->|Model fit not satisfactory|C
C[Choose/Modify Model] --> D[Specify Priors]
D --> E[Prior Predictive Check]
E --> G[MCMC Sampling with Convergence diagnostics]
G --> H[Posterior Predictive Check]
end
subgraph RESULTS
%% I -->|Model is reasonable|J[Model comparisons/averaging]
J[Model comparisons/averaging] --> K[Interpret and Visualize Results]
end
DATA --> MODEL
MODEL --> RESULTS
Choose a Model: Bernoulli
Data: \(y\) = survival status (0 = “A”, 1 = “D”)
Parameter: \(\theta\) = probability of “D”
Model equation: \(y_i \sim \text{Bern}(\theta)\) for \(i = 1, 2, \ldots, N\)
- The model states:
the sample data \(y\) follows a Bernoulli distribution with the common parameter \(\theta\)
Bernoulli Likelihood
Notice that there is no subscript for \(\theta\):
- The model assumes each observation has the same \(\theta\)
- I.e., the observations are exchangeable
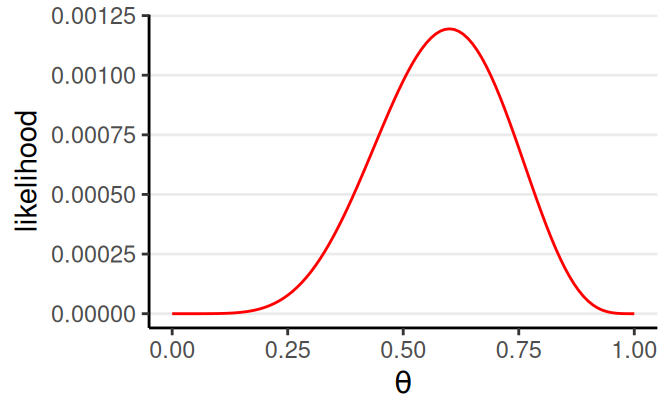
\[ P(y_1, y_2, \ldots, y_N) = \theta^z (1 - \theta)^{N - z} \]
\(z\) = number of “successes” (“D”)
- \(z\) = 6 in this illustrative sample
| theta | likelihood |
|---|---|
| 0.0 | 0.00000 |
| 0.1 | 0.00000 |
| 0.2 | 0.00003 |
| 0.3 | 0.00018 |
| 0.4 | 0.00053 |
| 0.5 | 0.00098 |
| 0.6 | 0.00119 |
| 0.7 | 0.00095 |
| 0.8 | 0.00042 |
| 0.9 | 0.00005 |
| 1.0 | 0.00000 |
Choosing Priors
When choosing priors, start with the support of the parameter(s)
- Support: Values that are possible
Support for \(\theta\): [0, 1]
One possible (but unlikely) option
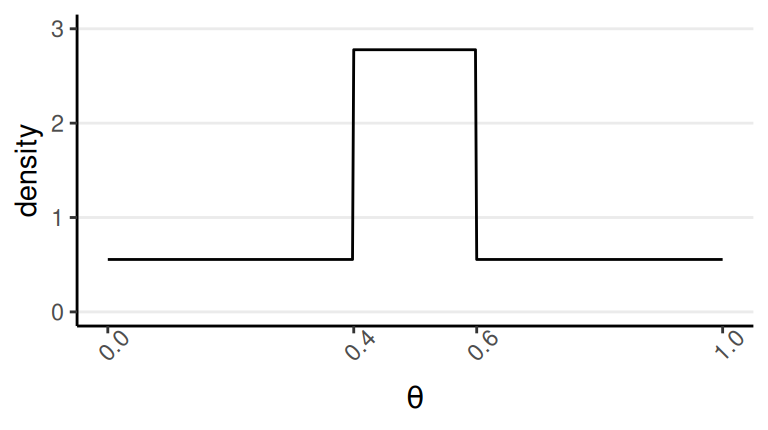
\(\theta\) values in the range \([.40, .60)\) are 5 times more likely than any values outside of that range
Conjugate Prior: Beta Distribution
\[ P(\theta \mid a, b) \propto \theta^{a - 1} (1 - \theta)^{b - 1} I_{[0, 1]} \]
Conjugate Prior
A prior distribution that yields posterior in the same distribution family as the prior
Two hyperparameters, \(a\) and \(b\):
- \(a - 1\) = number of prior ‘successes’ (e.g., “D”)
- \(b - 1\) = number of prior ‘failures’

More on the Beta Distribution
When \(a > b\), more density to the right (i.e., larger \(\theta\)), and vice versa
Mean = \(a / (a + b)\)
Concentration = \(\kappa = a + b\); \(\uparrow \kappa\), \(\downarrow\) variance, \(\uparrow\) strength of prior
E.g., A Beta(1, 1) prior means 0 prior success and 0 failure
- i.e., no prior information (i.e., noninformative)
Notes on Choosing Priors
Give \(>\) 0 probability/density for all possible values of a parameter
When the prior contains relatively little information
- different choices usually make little difference
Do a prior predictive check
Sensitivity analyses to see how sensitive results are to different reasonable prior choices.
Obtaining the Posterior Analytically
\[ P(\theta \mid y) = \frac{P(y \mid \theta) P(\theta)}{\int_0^1 P(y \mid \theta^*) P(\theta^*) d \theta^*} \]
The denominator is usually intractable
Conjugate prior: Posterior is from a known distribution family
- \(N\) trials and \(z\) successes
- \(\mathrm{Beta}(a, b)\) prior
- \(\Rightarrow\) \(\mathrm{Beta}(a + z, b + N - z)\) posterior
- \(a + \color{red}{z} - 1\) successes
- \(b + \color{red}{N - z} - 1\) failures
Back to the Example
\(N\) = 10, \(z\) = 6
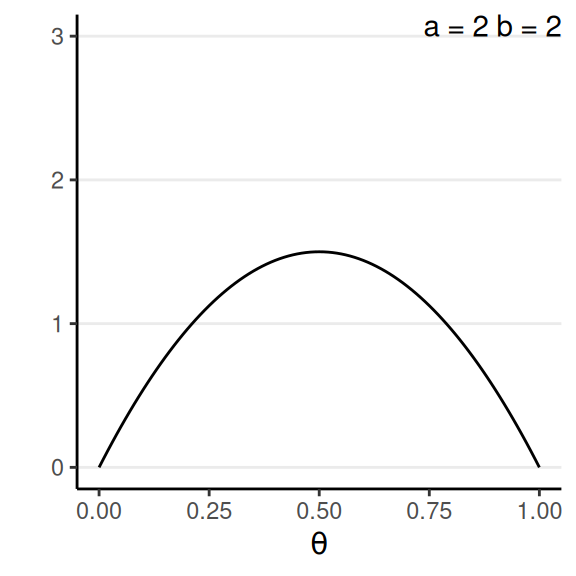
Prior: Do you believe that the fatality rate of AIDS is 100%? or 0%?
- Let’s use \(\kappa = 4\), prior mean = 0.5, so \(a\) = 2 and \(b\) = 2
Posterior Beta
\[ \theta \mid y \sim \mathrm{Beta}(2 + 6, 2 + 4) \]

Summarizing the Posterior
If the posterior is from a known family, one can evalue summary statistics analytically
- E.g., \(E(\theta \mid y) = \int_0^1 \theta P(\theta \mid y) d \theta\)
However, more often, a simulation-based approach is used to draw samples from the posterior
| Statistic | Common Name | Value |
|---|---|---|
| mean | Bayes estimate/Expected a posteriori (EAP) | 0.563 |
| median | Posterior median | 0.567 |
| mode | Maximum a posteriori (MAP) | 0.577 |
| SD | Posterior SD | 0.126 |
| MAD | Posterior MAD | 0.13 |
| 80% CI | (Equal-tailed) Credible interval | [0.398, 0.727] |
| 80% HDI | HDI/Highest Posterior Density Interval (HPDI) | [0.404, 0.733] |
Using the Full Data
1082 A, 1761 D \(\rightarrow\) \(N\) = 2843, \(z\) = 1761
Posterior: Beta(1763, 1084)
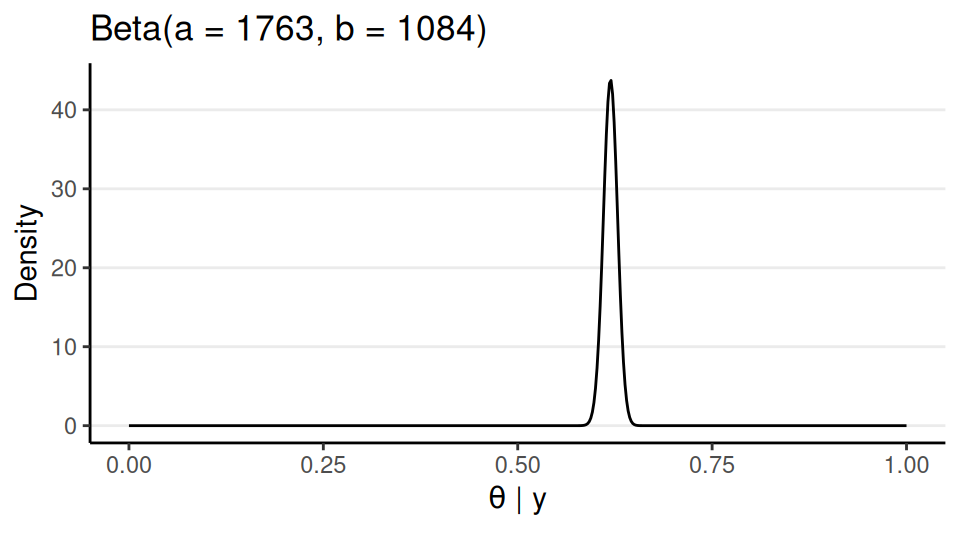
Posterior Predictive Check
Posterior Predictive Distribution
\[ P(\tilde y \mid y) = \int P(\tilde y \mid \theta, y) P(\theta \mid y) d \theta \]
- \(\tilde y\) = new/future data
Simulate a new \(\theta^*\) from posterior, then simulate a new data set
If the model does not fit the data, any results are basically meaningless at best, and can be very misleading
Requires substantive knowledge and some creativity
- E.g., are the case fatality rates equal across the 4 state categories?
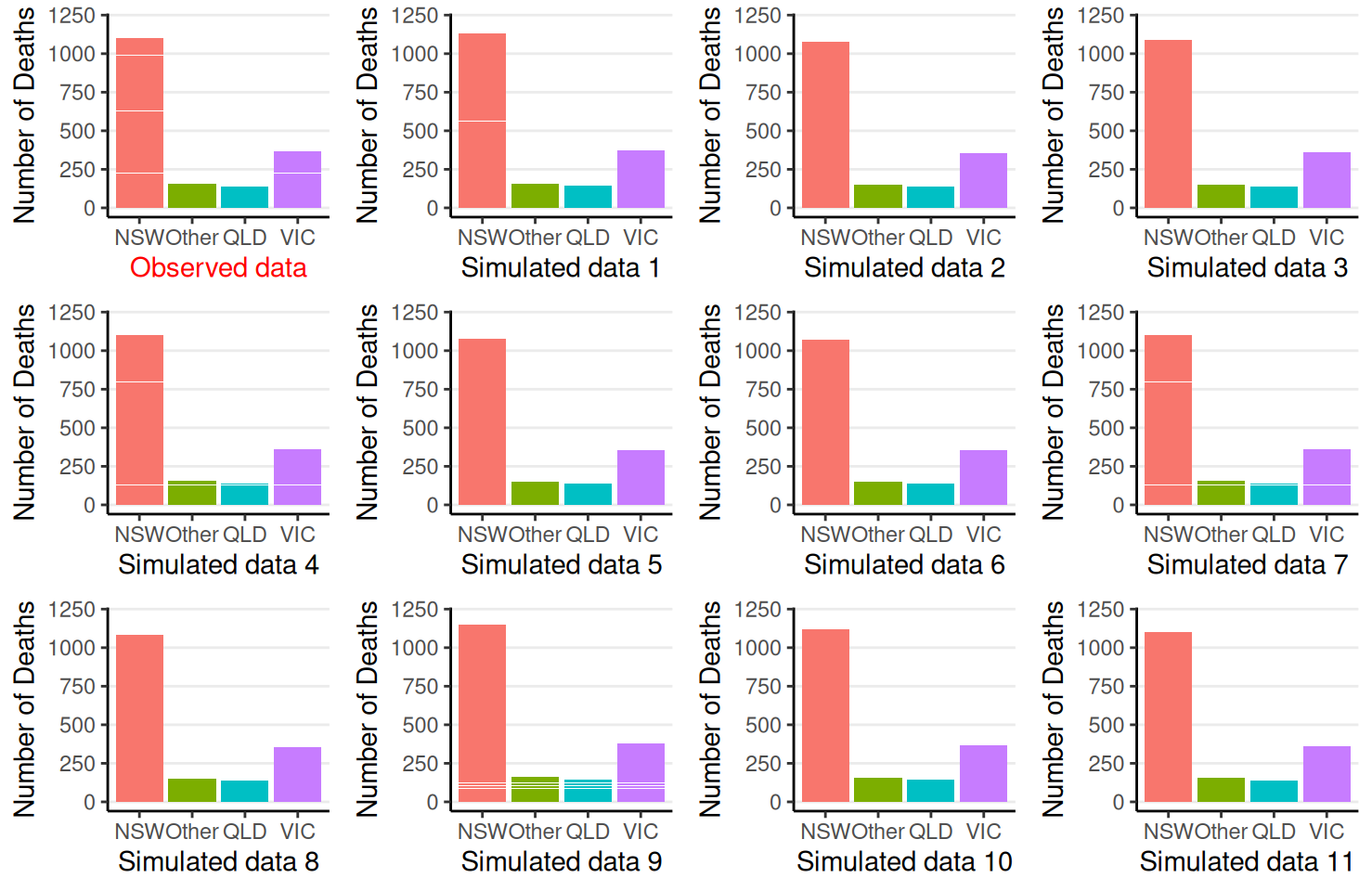
Some Common Checks
- Does the model simulate data with similar distributions as the observed data?
- e.g., skewness, range
- Subsets of observed data that are of more interest?
- e.g., old age group
- If not fit, age should be incorporated in the model
See an example in Gabry et al. (2019)
Stan
See notes
Stan Example
Example Check: Sample mean by age group
Here we use the function bayesplot::ppc_stat_grouped()
1age50 <- factor(Aids2$age > 50, labels = c("<= 50", "> 50"))
2bern_pp_fit$draws("ytilde", format = "draws_matrix") |>
3 ppc_stat_grouped(y = Aids2_standata$y, group = age50, stat = "mean")- 1
- Create binary indicator of two age groups
- 2
- Extract simulated data sets
- 3
- Plot a histogram of the sample means from the simulated data (i.e., posterior predictive distribution) for each age group
Other One-Parameter Models
Binomial Model
- For count outcome: \(y_i \sim \mathrm{Bin}(N_i, \theta)\)
- \(\theta\): rate of occurrence (per trial)
- Conjugate prior: Beta
- E.g.,
- \(y\) minority candidates in \(N\) new hires
- \(y\) out of \(N\) symptoms checked
- A word appears \(y\) times in a tweet of \(N\) number of words
Poisson Model
- For count outcome: \(y_i \sim \mathrm{Pois}(\theta)\)
- \(\theta\): rate of occurrence
- Conjugate prior: Gamma
- E.g.,
- Drinking \(y\) times in a week
- \(y\) hate crimes in a year for a county
- \(y\) people visiting a store in an hour