library(here)
library(haven) # for reading SPSS data
library(tidyverse)
library(lme4)Warning in check_dep_version(): ABI version mismatch:
lme4 was built with Matrix ABI version 2
Current Matrix ABI version is 1
Please re-install lme4 from source or restore original 'Matrix' packageThis second example comes from the companion website of the textbook, which can be downloaded here: https://www.guilford.com/companion-site/Measurement-Theory-and-Applications-for-the-Social-Sciences/9781462532131
The file you need is the SPSS zip file from Chapter 10.
# Import data
# Assume you downloaded the data to the folder "data", with the name
# "Bandalos_Ch10_SPSS.zip"
zip_data <- here("data", "Bandalos_Ch10_SPSS.zip")
if (!file.exists(zip_data)) {
dir.create("data")
download.file(
"https://www.guilford.com/add/bandalos/Bandalos_Ch10_SPSS.zip",
zip_data
)
}
sample_data <- read_sav(
unz(
zip_data,
"Bandalos_Ch10_SPSS/Data/Table 10.4 data untransposed.sav"
)
)
sample_dataWhile it’s possible to run analyses using the wide format, for our analyses we’ll transform the data to a long format as it better suits the analytic framework (variance components model) we’ll use. This also has better handling for missing data.
We’ll use the pivot_longer() function from the tidyr package (which is loaded with library(tidyverse)).
sample_long <- pivot_longer(
sample_data,
# select all columns, except the 1st one to be transformed
cols = -1,
# The columns have a pattern "R(1)Task(2)", where values
# in parentheses are the IDs for the facets. So we first
# specify this pattern, with a "." meaning a one-digit
# place holder,
names_pattern = "R(.)Task(.)",
# and then specify that the first place holder is for rater,
# and the second place-holder is for task.
names_to = c("rater", "task"),
values_to = "score" # name of score variable
)
head(sample_long)As can be seen, the data are now in a long format.
The data here has each participant (p) rated by the same three raters (r) on each of the three tasks (t). Therefore, this is a p \(\times\) r \(\times\) t design, where the two facets are crossed. We can see this by looking at the following tables:
with(sample_long,
table(person, rater)) rater
person 1 2 3
1 3 3 3
2 3 3 3
3 3 3 3
4 3 3 3
5 3 3 3
6 3 3 3
7 3 3 3
8 3 3 3
9 3 3 3
10 3 3 3
11 3 3 3
12 3 3 3with(sample_long,
table(rater, task)) task
rater 1 2 3
1 12 12 12
2 12 12 12
3 12 12 12with(sample_long,
table(person, task)) task
person 1 2 3
1 3 3 3
2 3 3 3
3 3 3 3
4 3 3 3
5 3 3 3
6 3 3 3
7 3 3 3
8 3 3 3
9 3 3 3
10 3 3 3
11 3 3 3
12 3 3 3With a crossed (factorial) design, every cell should be filled.
On the other hand, if we have different sets of raters for different tasks, we will have a nested design. Let’s say we actually have 9 raters, with raters 1-3 for task 1, raters 4-6 for task 2, and raters 7-9 for task 3. This yields a p \(\times\) (r:t) design with raters nested within tasks.
# Recode raters
sample2 <- sample_long |>
group_by(person) |>
mutate(actual_rater = 1:9) |>
ungroup()
with(sample2,
table(person, actual_rater)) actual_rater
person 1 2 3 4 5 6 7 8 9
1 1 1 1 1 1 1 1 1 1
2 1 1 1 1 1 1 1 1 1
3 1 1 1 1 1 1 1 1 1
4 1 1 1 1 1 1 1 1 1
5 1 1 1 1 1 1 1 1 1
6 1 1 1 1 1 1 1 1 1
7 1 1 1 1 1 1 1 1 1
8 1 1 1 1 1 1 1 1 1
9 1 1 1 1 1 1 1 1 1
10 1 1 1 1 1 1 1 1 1
11 1 1 1 1 1 1 1 1 1
12 1 1 1 1 1 1 1 1 1with(sample2,
table(actual_rater, task)) task
actual_rater 1 2 3
1 12 0 0
2 0 12 0
3 0 0 12
4 12 0 0
5 0 12 0
6 0 0 12
7 12 0 0
8 0 12 0
9 0 0 12with(sample2,
table(person, task)) task
person 1 2 3
1 3 3 3
2 3 3 3
3 3 3 3
4 3 3 3
5 3 3 3
6 3 3 3
7 3 3 3
8 3 3 3
9 3 3 3
10 3 3 3
11 3 3 3
12 3 3 3When facet A is nested in facet B (i.e., a:b), each level of A is associated with only one level of B, but each level of B is associated with multiple levels of A.
m1 <- lmer(
score ~ 1 +
(1 | person) + (1 | rater) + (1 | task) +
(1 | person:rater) + (1 | person:task) +
(1 | rater:task),
data = sample_long
)boundary (singular) fit: see help('isSingular')# Variance components (VCs)
vc_m1 <- as.data.frame(VarCorr(m1))
# Organize in a table, similar to Table 10.4
data.frame(source = vc_m1$grp,
var = vc_m1$vcov,
percent = vc_m1$vcov / sum(vc_m1$vcov))get_vc <- function(x) {
vc_x <- as.data.frame(VarCorr(x))
c(vc_x$vcov, vc_x$vcov / sum(vc_x$vcov))
}
boo <- bootMer(m1, FUN = get_vc, nsim = 1999)
# Get percentile CIs for person variance
boot::boot.ci(boo, type = "perc", index = 3)BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1999 bootstrap replicates
CALL :
boot::boot.ci(boot.out = boo, type = "perc", index = 3)
Intervals :
Level Percentile
95% ( 0.171, 2.364 )
Calculations and Intervals on Original Scale# Get percentile CIs for proportion of person variance
boot::boot.ci(boo, type = "perc", index = 10)BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1999 bootstrap replicates
CALL :
boot::boot.ci(boot.out = boo, type = "perc", index = 10)
Intervals :
Level Percentile
95% ( 0.1107, 0.6659 )
Calculations and Intervals on Original Scale# Get percentile CIs for all VCs
ci_vc <- lapply(1:14, FUN = function(i) {
ci_i <- boot::boot.ci(boo, type = "perc", index = i)$percent
c(ll_var = ci_i[4], ul_var = ci_i[5])
})It also helps to create a function so that we can do the same operation in the future:
table_vc <- function(x, digits = 2) {
vc_x <- as.data.frame(VarCorr(x))
out <- data.frame(
source = vc_x$grp,
sd = sqrt(vc_x$vcov),
var = vc_x$vcov,
percent = vc_x$vcov / sum(vc_x$vcov))
print(out, digits = digits)
}
table_vc(m1) source sd var percent
1 person:task 0.35 0.119 0.0511
2 person:rater 0.68 0.468 0.2003
3 person 1.02 1.036 0.4432
4 rater:task 0.11 0.012 0.0049
5 task 0.25 0.061 0.0262
6 rater 0.00 0.000 0.0000
7 Residual 0.80 0.641 0.2743# Add CIs
cbind(table_vc(m1),
do.call(rbind, ci_vc[1:7]),
prop = do.call(rbind, ci_vc[8:14])) |>
print(digits = 2) source sd var percent
1 person:task 0.35 0.119 0.0511
2 person:rater 0.68 0.468 0.2003
3 person 1.02 1.036 0.4432
4 rater:task 0.11 0.012 0.0049
5 task 0.25 0.061 0.0262
6 rater 0.00 0.000 0.0000
7 Residual 0.80 0.641 0.2743
source sd var percent ll_var ul_var prop.ll_var prop.ul_var
1 person:task 0.35 0.119 0.0511 0.00 0.35 0.000 0.166
2 person:rater 0.68 0.468 0.2003 0.12 0.86 0.052 0.404
3 person 1.02 1.036 0.4432 0.17 2.36 0.111 0.666
4 rater:task 0.11 0.012 0.0049 0.00 0.10 0.000 0.048
5 task 0.25 0.061 0.0262 0.00 0.32 0.000 0.132
6 rater 0.00 0.000 0.0000 0.00 0.16 0.000 0.067
7 Residual 0.80 0.641 0.2743 0.41 0.87 0.144 0.491As shown above, while universe score variance (person variance) is the largest, it only accounts for a proportion of 0.4431584 of the total variance. If we use teminology analogous to classical test theory, it means that if we use a single rating of a single task to generalize to the universe score, less than half of the observed score variance is due to true score variance.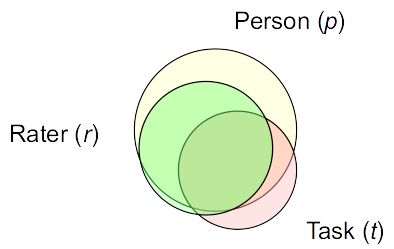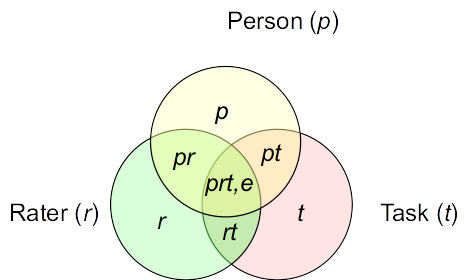
E.g., The ratings are on a 6-point scale. With \(\hat \sigma_{pr}\) = 0.6841528, this is the margin of error due to rater-by-person interaction, which is not trivial.
# If treating task as fixed, the person x task variance will be averaged
# and become part of the universe score
varu <- vc_m1$vcov[3] + vc_m1$vcov[1] / 3
# The rater x task variance will be averaged and become part of rater variance
varr <- vc_m1$vcov[6] + vc_m1$vcov[4] / 3
# The residual will be averaged and become part of person x rater variance
vare <- vc_m1$vcov[2] + vc_m1$vcov[7] / 3
# Combine
data.frame(source = vc_m1$grp[c(3, 6, 2)],
var = c(varu, varr, vare),
percent = c(varu, varr, vare) / sum(varu, varr, vare))mean_scores <- rowMeans(sample_data[-1])
dep_coef <- function(x) {
vc_x <- as.data.frame(VarCorr(x))
# G coefficient (for relative decision)
g_coef <- with(
vc_x,
vcov[3] / (vcov[3] + vcov[1] / 3 + vcov[2] / 3 + vcov[7] / 3 / 3)
)
# phi coefficient (for absolute decision)
phi_coef <- with(
vc_x,
vcov[3] /
(vcov[3] + vcov[1] / 3 + vcov[2] / 3 +
vcov[7] / 3 / 3 +
vcov[4] / 3 / 3 + vcov[5] / 3 + vcov[6] / 3)
)
c(g = g_coef, phi = phi_coef)
}
dep_coef(m1) g phi
0.7950021 0.7819758