Item Response Theory

library(mirt)

Rasch Model

data(LSAT7, package = "mirt")
dat <- expand.table(LSAT7)

m_rasch <- mirt(dat, model = 1, itemtype = "Rasch")


Iteration: 1, Log-Lik: -2664.942, Max-Change: 0.01075
Iteration: 2, Log-Lik: -2664.913, Max-Change: 0.00257
Iteration: 3, Log-Lik: -2664.910, Max-Change: 0.00210
Iteration: 4, Log-Lik: -2664.908, Max-Change: 0.00179
Iteration: 5, Log-Lik: -2664.906, Max-Change: 0.00156
Iteration: 6, Log-Lik: -2664.905, Max-Change: 0.00137
Iteration: 7, Log-Lik: -2664.904, Max-Change: 0.00141
Iteration: 8, Log-Lik: -2664.903, Max-Change: 0.00110
Iteration: 9, Log-Lik: -2664.903, Max-Change: 0.00095
Iteration: 10, Log-Lik: -2664.902, Max-Change: 0.00086
Iteration: 11, Log-Lik: -2664.902, Max-Change: 0.00072
Iteration: 12, Log-Lik: -2664.902, Max-Change: 0.00063
Iteration: 13, Log-Lik: -2664.902, Max-Change: 0.00065
Iteration: 14, Log-Lik: -2664.901, Max-Change: 0.00051
Iteration: 15, Log-Lik: -2664.901, Max-Change: 0.00044
Iteration: 16, Log-Lik: -2664.901, Max-Change: 0.00040
Iteration: 17, Log-Lik: -2664.901, Max-Change: 0.00034
Iteration: 18, Log-Lik: -2664.901, Max-Change: 0.00029
Iteration: 19, Log-Lik: -2664.901, Max-Change: 0.00030
Iteration: 20, Log-Lik: -2664.901, Max-Change: 0.00024
Iteration: 21, Log-Lik: -2664.901, Max-Change: 0.00020
Iteration: 22, Log-Lik: -2664.901, Max-Change: 0.00018
Iteration: 23, Log-Lik: -2664.901, Max-Change: 0.00016
Iteration: 24, Log-Lik: -2664.901, Max-Change: 0.00014
Iteration: 25, Log-Lik: -2664.901, Max-Change: 0.00014
Iteration: 26, Log-Lik: -2664.901, Max-Change: 0.00011
Iteration: 27, Log-Lik: -2664.901, Max-Change: 0.00009

coef(m_rasch, IRTpars = TRUE, simplify = TRUE) # d = intercept = -1 * difficulty

$items
       a      b g u
Item.1 1 -1.868 0 1
Item.2 1 -0.791 0 1
Item.3 1 -1.461 0 1
Item.4 1 -0.521 0 1
Item.5 1 -1.993 0 1

$means
F1 
 0 

$cov
      F1
F1 1.022

The 1PL is just a reparameterization of the Rasch model:

# 1PL
mod_1pl <- "
THETA = 1-5
CONSTRAIN = (1-5, a1)
"
m_1pl <- mirt(dat, mod_1pl)


Iteration: 1, Log-Lik: -2668.786, Max-Change: 0.06198
Iteration: 2, Log-Lik: -2666.196, Max-Change: 0.03935
Iteration: 3, Log-Lik: -2665.347, Max-Change: 0.02405
Iteration: 4, Log-Lik: -2664.955, Max-Change: 0.00867
Iteration: 5, Log-Lik: -2664.920, Max-Change: 0.00509
Iteration: 6, Log-Lik: -2664.907, Max-Change: 0.00294
Iteration: 7, Log-Lik: -2664.902, Max-Change: 0.00135
Iteration: 8, Log-Lik: -2664.901, Max-Change: 0.00079
Iteration: 9, Log-Lik: -2664.901, Max-Change: 0.00046
Iteration: 10, Log-Lik: -2664.901, Max-Change: 0.00022
Iteration: 11, Log-Lik: -2664.901, Max-Change: 0.00011
Iteration: 12, Log-Lik: -2664.901, Max-Change: 0.00006

coef(m_1pl, IRTpars = TRUE, simplify = TRUE) # b = difficulty

$items
           a      b g u
Item.1 1.011 -1.848 0 1
Item.2 1.011 -0.782 0 1
Item.3 1.011 -1.445 0 1
Item.4 1.011 -0.516 0 1
Item.5 1.011 -1.971 0 1

$means
THETA 
    0 

$cov
      THETA
THETA     1

What is the relationship between (a) the estimated variance of the latent variable (labelled “COV_11”) in the 1PL model and (b) the \(a\) parameter in the Rasch model?

Your answer:

Standard Errors

m_rasch <- mirt(dat, model = 1, itemtype = "Rasch", SE = TRUE)


Iteration: 1, Log-Lik: -2664.942, Max-Change: 0.01075
Iteration: 2, Log-Lik: -2664.913, Max-Change: 0.00257
Iteration: 3, Log-Lik: -2664.910, Max-Change: 0.00210
Iteration: 4, Log-Lik: -2664.908, Max-Change: 0.00179
Iteration: 5, Log-Lik: -2664.906, Max-Change: 0.00156
Iteration: 6, Log-Lik: -2664.905, Max-Change: 0.00137
Iteration: 7, Log-Lik: -2664.904, Max-Change: 0.00141
Iteration: 8, Log-Lik: -2664.903, Max-Change: 0.00110
Iteration: 9, Log-Lik: -2664.903, Max-Change: 0.00095
Iteration: 10, Log-Lik: -2664.902, Max-Change: 0.00086
Iteration: 11, Log-Lik: -2664.902, Max-Change: 0.00072
Iteration: 12, Log-Lik: -2664.902, Max-Change: 0.00063
Iteration: 13, Log-Lik: -2664.902, Max-Change: 0.00065
Iteration: 14, Log-Lik: -2664.901, Max-Change: 0.00051
Iteration: 15, Log-Lik: -2664.901, Max-Change: 0.00044
Iteration: 16, Log-Lik: -2664.901, Max-Change: 0.00040
Iteration: 17, Log-Lik: -2664.901, Max-Change: 0.00034
Iteration: 18, Log-Lik: -2664.901, Max-Change: 0.00029
Iteration: 19, Log-Lik: -2664.901, Max-Change: 0.00030
Iteration: 20, Log-Lik: -2664.901, Max-Change: 0.00024
Iteration: 21, Log-Lik: -2664.901, Max-Change: 0.00020
Iteration: 22, Log-Lik: -2664.901, Max-Change: 0.00018
Iteration: 23, Log-Lik: -2664.901, Max-Change: 0.00016
Iteration: 24, Log-Lik: -2664.901, Max-Change: 0.00014
Iteration: 25, Log-Lik: -2664.901, Max-Change: 0.00014
Iteration: 26, Log-Lik: -2664.901, Max-Change: 0.00011
Iteration: 27, Log-Lik: -2664.901, Max-Change: 0.00009

Calculating information matrix...

coef(m_rasch, IRTpars = TRUE)

$Item.1
         a      b  g  u
par      1 -1.868  0  1
CI_2.5  NA -2.065 NA NA
CI_97.5 NA -1.671 NA NA

$Item.2
         a      b  g  u
par      1 -0.791  0  1
CI_2.5  NA -0.950 NA NA
CI_97.5 NA -0.632 NA NA

$Item.3
         a      b  g  u
par      1 -1.461  0  1
CI_2.5  NA -1.640 NA NA
CI_97.5 NA -1.282 NA NA

$Item.4
         a      b  g  u
par      1 -0.521  0  1
CI_2.5  NA -0.676 NA NA
CI_97.5 NA -0.367 NA NA

$Item.5
         a      b  g  u
par      1 -1.993  0  1
CI_2.5  NA -2.196 NA NA
CI_97.5 NA -1.790 NA NA

$GroupPars
        MEAN_1 COV_11
par          0  1.022
CI_2.5      NA  0.765
CI_97.5     NA  1.279

Plots

Item Response Function

Also item characteristic curve

plot(m_rasch, type = "trace")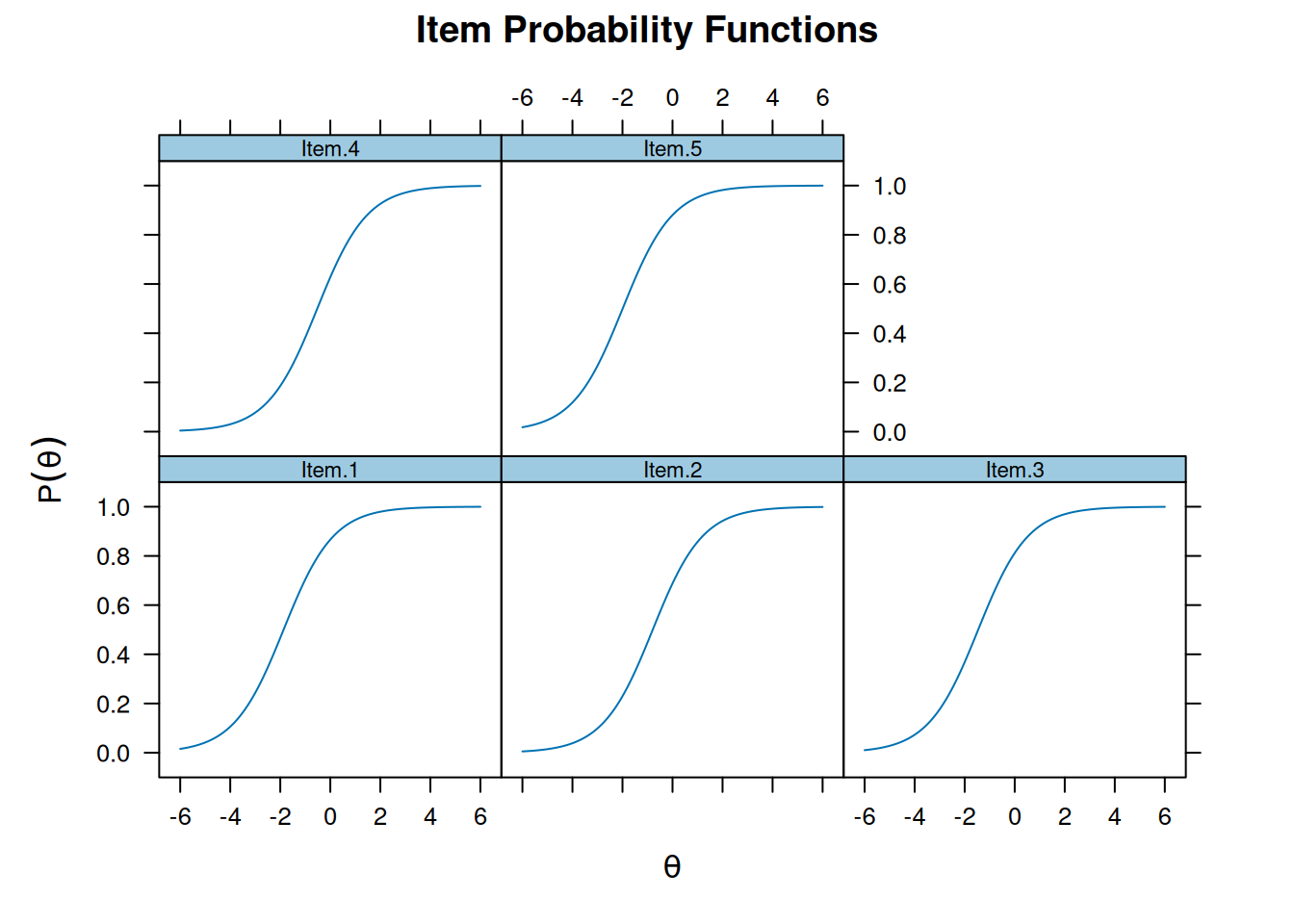

Item and Test Information

Item information

plot(m_rasch, type = "infotrace")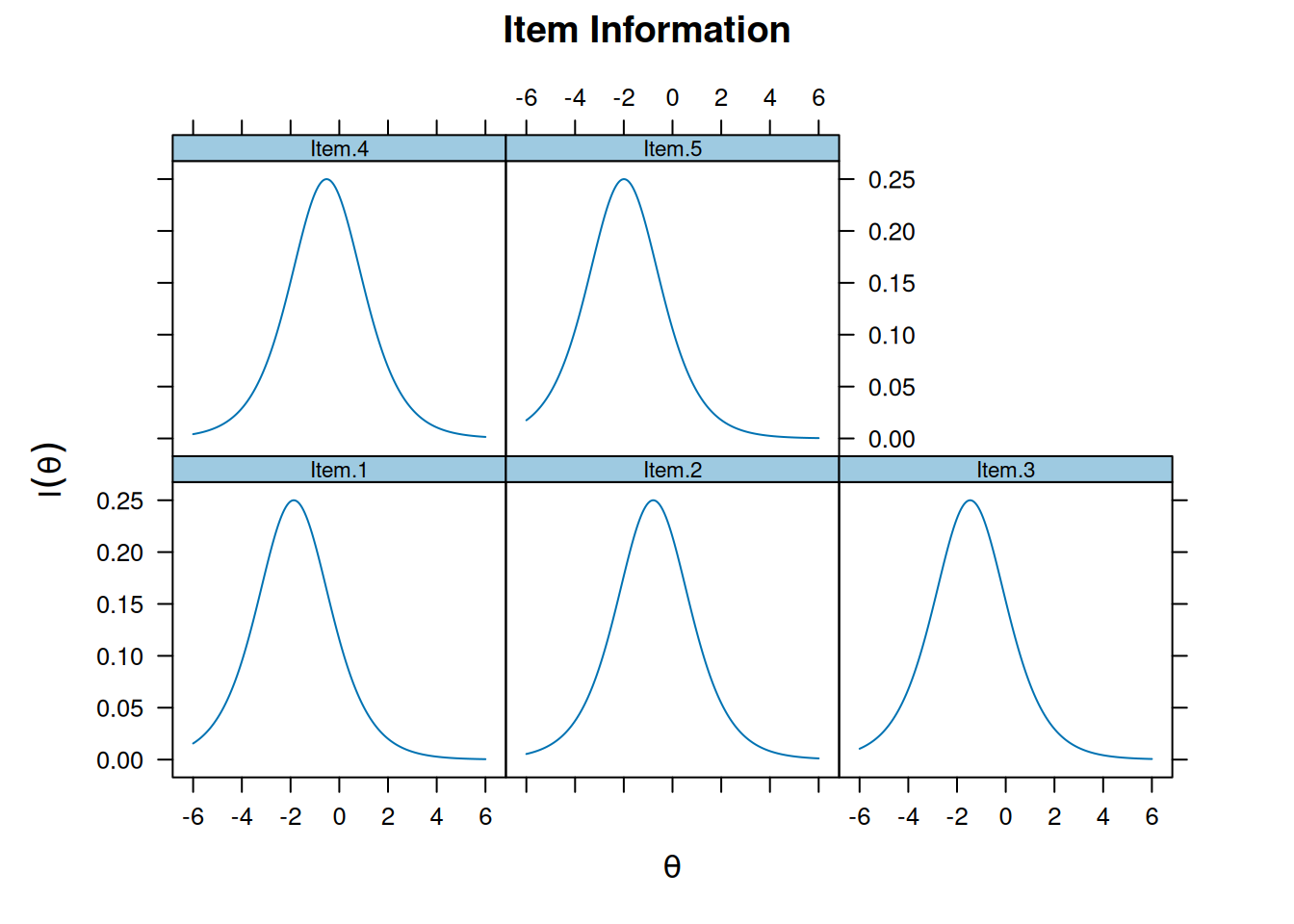

plot(m_rasch, type = "info")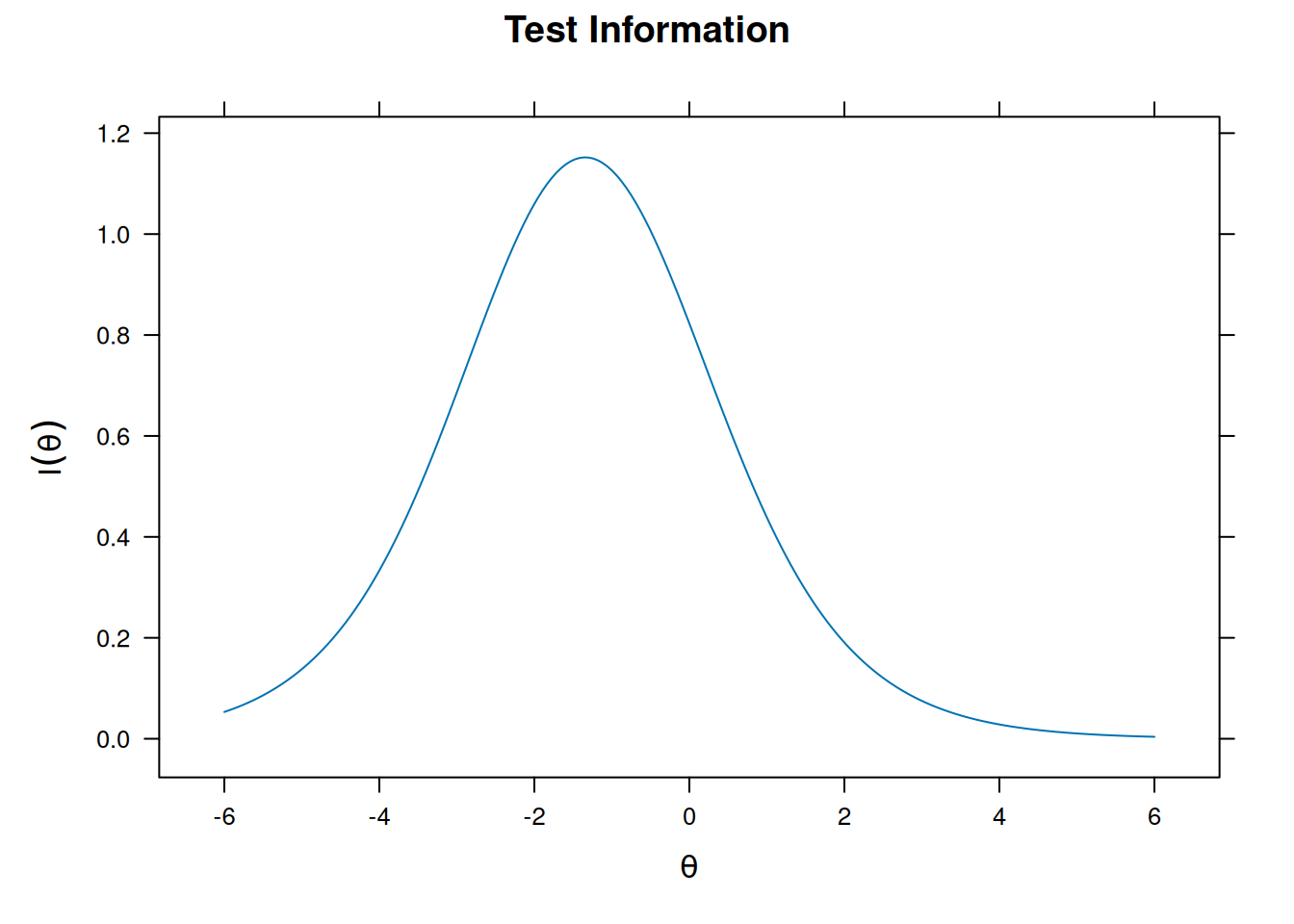

In IRT, the reliability is typically different across different levels of \(\theta\). One way to compute reliability that is comparable to the reliability coefficient in CTT is

\[\text{Reliability} = \frac{Var(\theta)}{Var(\theta) + 1 / I(\theta)}\]

What level of \(\theta\) corresponds to the highest reliability in the Rasch model, and what value is the reliability coefficient?

Your answer:

Assumptions/Model Fit

Global test statistics (analogous to those in factor analysis)

\(G^2\) test statistic (not valid when matrix is sparse)
\(M_2\): better approximation for polytomous models

m_rasch


Call:
mirt(data = dat, model = 1, itemtype = "Rasch", SE = TRUE)

Full-information item factor analysis with 1 factor(s).
Converged within 1e-04 tolerance after 27 EM iterations.
mirt version: 1.41 
M-step optimizer: nlminb 
EM acceleration: Ramsay 
Number of rectangular quadrature: 61
Latent density type: Gaussian 

Information matrix estimated with method: Oakes
Second-order test: model is a possible local maximum
Condition number of information matrix =  4.488772

Log-likelihood = -2664.901
Estimated parameters: 6 
AIC = 5341.802
BIC = 5371.248; SABIC = 5352.192
G2 (25) = 43.89, p = 0.0112
RMSEA = 0.028, CFI = NaN, TLI = NaN

M2(m_rasch)

Parallel analysis

psych::fa.parallel(dat, cor = "poly", fa = "pc")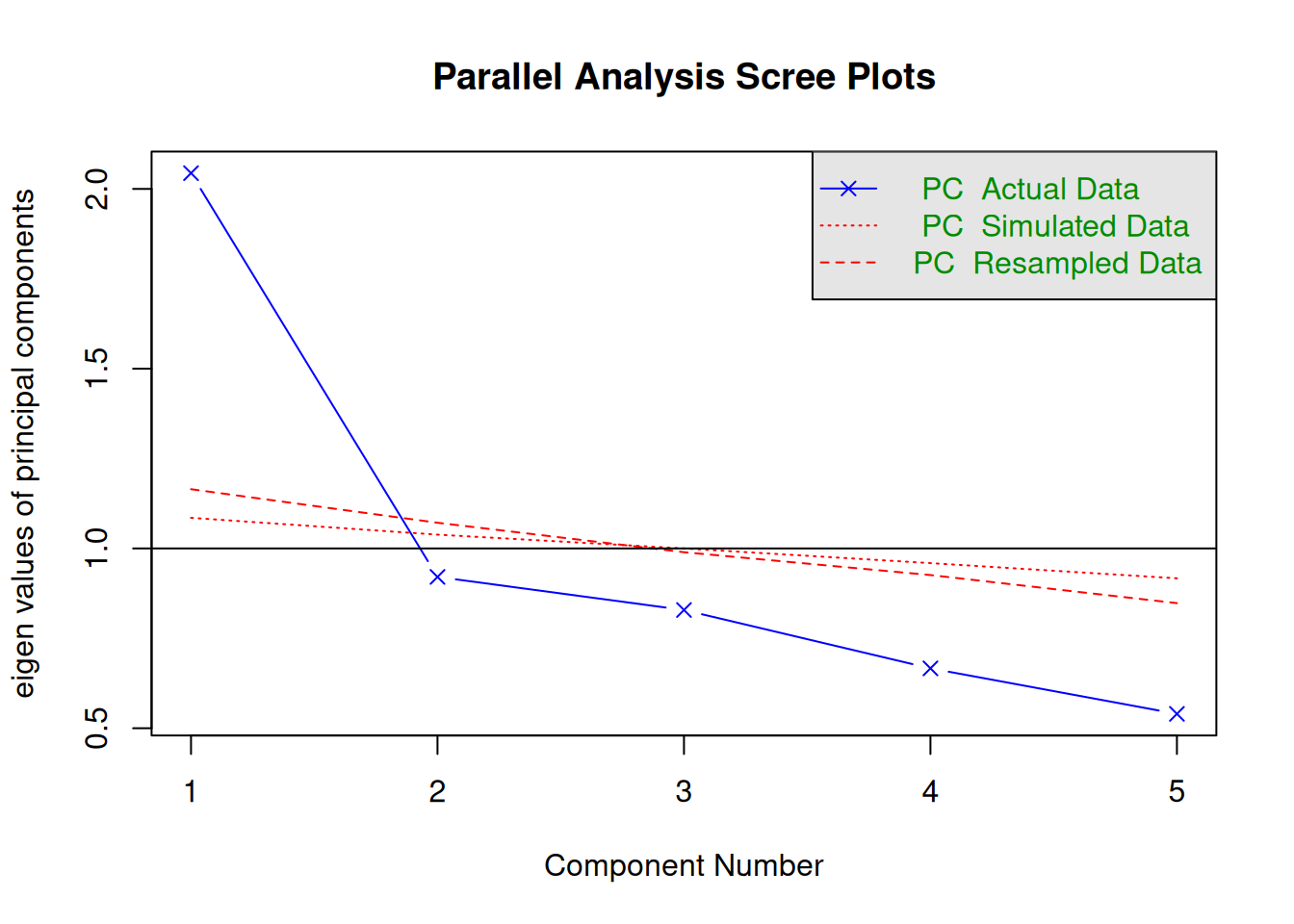

Parallel analysis suggests that the number of factors =  NA  and the number of components =  1

Local Independence

residuals(m_rasch, type = "Q3")  # Q3

Q3 summary statistics:
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 -0.196  -0.145  -0.116  -0.110  -0.082   0.000 

       Item.1 Item.2 Item.3 Item.4 Item.5
Item.1  1.000 -0.136 -0.099 -0.080 -0.051
Item.2 -0.136  1.000  0.000 -0.196 -0.169
Item.3 -0.099  0.000  1.000 -0.133 -0.090
Item.4 -0.080 -0.196 -0.133  1.000 -0.149
Item.5 -0.051 -0.169 -0.090 -0.149  1.000

# All |Q3| < .2 in this case

Item Fit

S-\(\chi^2\)

itemfit(m_rasch)

# For large number of items, the p values should be adjusted
itemfit(m_rasch, p.adjust = "holm")

Which item(s) are not fitting well with the Rasch model?

Your answer:

Two-Parameter Logistic

m_2pl <- mirt(dat, model = 1, itemtype = "2PL")


Iteration: 1, Log-Lik: -2668.786, Max-Change: 0.18243
Iteration: 2, Log-Lik: -2663.691, Max-Change: 0.13637
Iteration: 3, Log-Lik: -2661.454, Max-Change: 0.10231
Iteration: 4, Log-Lik: -2659.430, Max-Change: 0.04181
Iteration: 5, Log-Lik: -2659.241, Max-Change: 0.03417
Iteration: 6, Log-Lik: -2659.113, Max-Change: 0.02911
Iteration: 7, Log-Lik: -2658.812, Max-Change: 0.00456
Iteration: 8, Log-Lik: -2658.809, Max-Change: 0.00363
Iteration: 9, Log-Lik: -2658.808, Max-Change: 0.00273
Iteration: 10, Log-Lik: -2658.806, Max-Change: 0.00144
Iteration: 11, Log-Lik: -2658.806, Max-Change: 0.00118
Iteration: 12, Log-Lik: -2658.806, Max-Change: 0.00101
Iteration: 13, Log-Lik: -2658.805, Max-Change: 0.00042
Iteration: 14, Log-Lik: -2658.805, Max-Change: 0.00025
Iteration: 15, Log-Lik: -2658.805, Max-Change: 0.00026
Iteration: 16, Log-Lik: -2658.805, Max-Change: 0.00023
Iteration: 17, Log-Lik: -2658.805, Max-Change: 0.00023
Iteration: 18, Log-Lik: -2658.805, Max-Change: 0.00021
Iteration: 19, Log-Lik: -2658.805, Max-Change: 0.00019
Iteration: 20, Log-Lik: -2658.805, Max-Change: 0.00017
Iteration: 21, Log-Lik: -2658.805, Max-Change: 0.00017
Iteration: 22, Log-Lik: -2658.805, Max-Change: 0.00015
Iteration: 23, Log-Lik: -2658.805, Max-Change: 0.00015
Iteration: 24, Log-Lik: -2658.805, Max-Change: 0.00013
Iteration: 25, Log-Lik: -2658.805, Max-Change: 0.00013
Iteration: 26, Log-Lik: -2658.805, Max-Change: 0.00011
Iteration: 27, Log-Lik: -2658.805, Max-Change: 0.00011
Iteration: 28, Log-Lik: -2658.805, Max-Change: 0.00010

coef(m_2pl, IRTpars = TRUE, simplify = TRUE)

$items
           a      b g u
Item.1 0.988 -1.879 0 1
Item.2 1.081 -0.748 0 1
Item.3 1.706 -1.058 0 1
Item.4 0.765 -0.635 0 1
Item.5 0.736 -2.520 0 1

$means
F1 
 0 

$cov
   F1
F1  1

plot(m_rasch, type = "trace", facet_items = FALSE)
plot(m_2pl, type = "trace", facet_items = FALSE)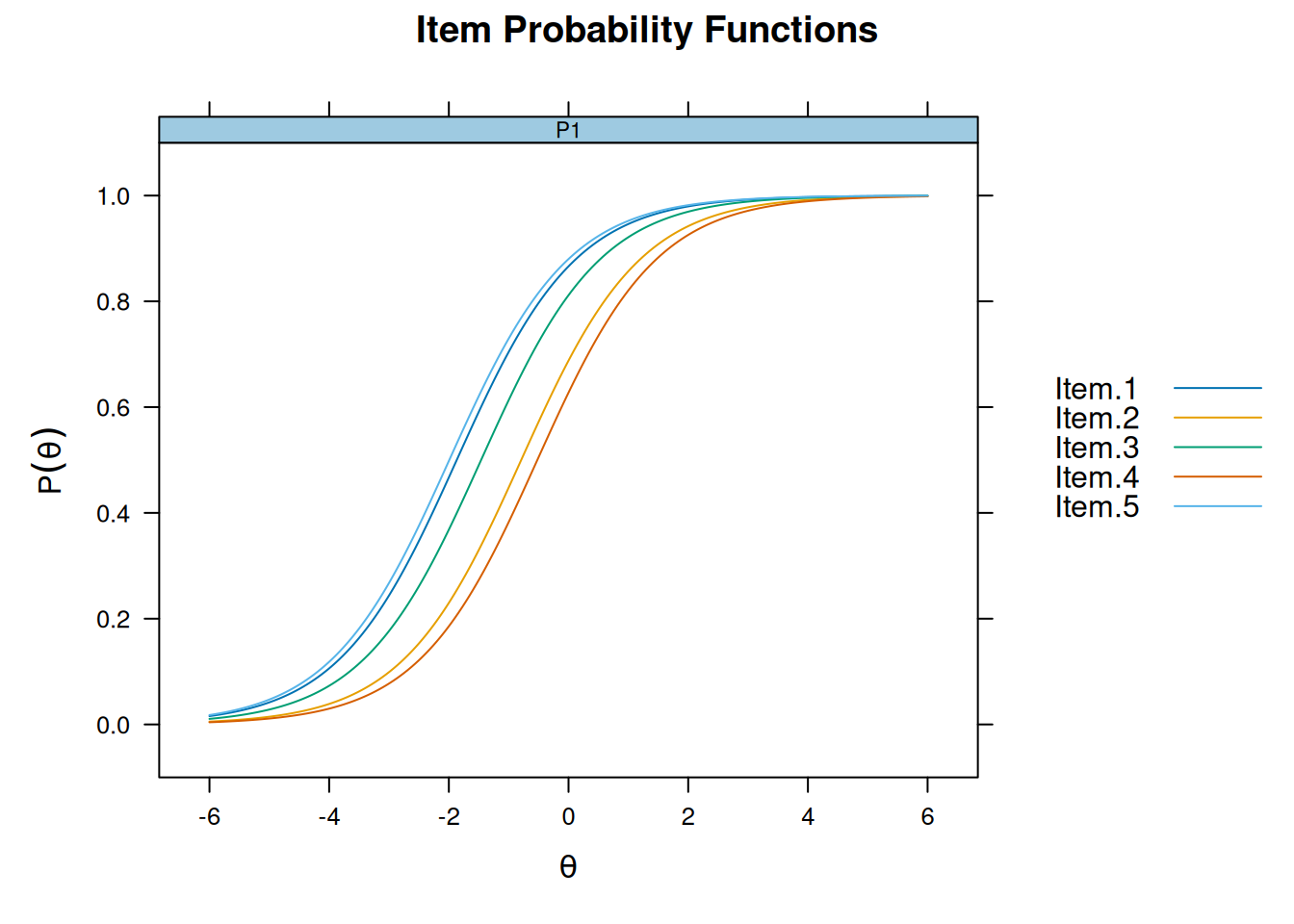

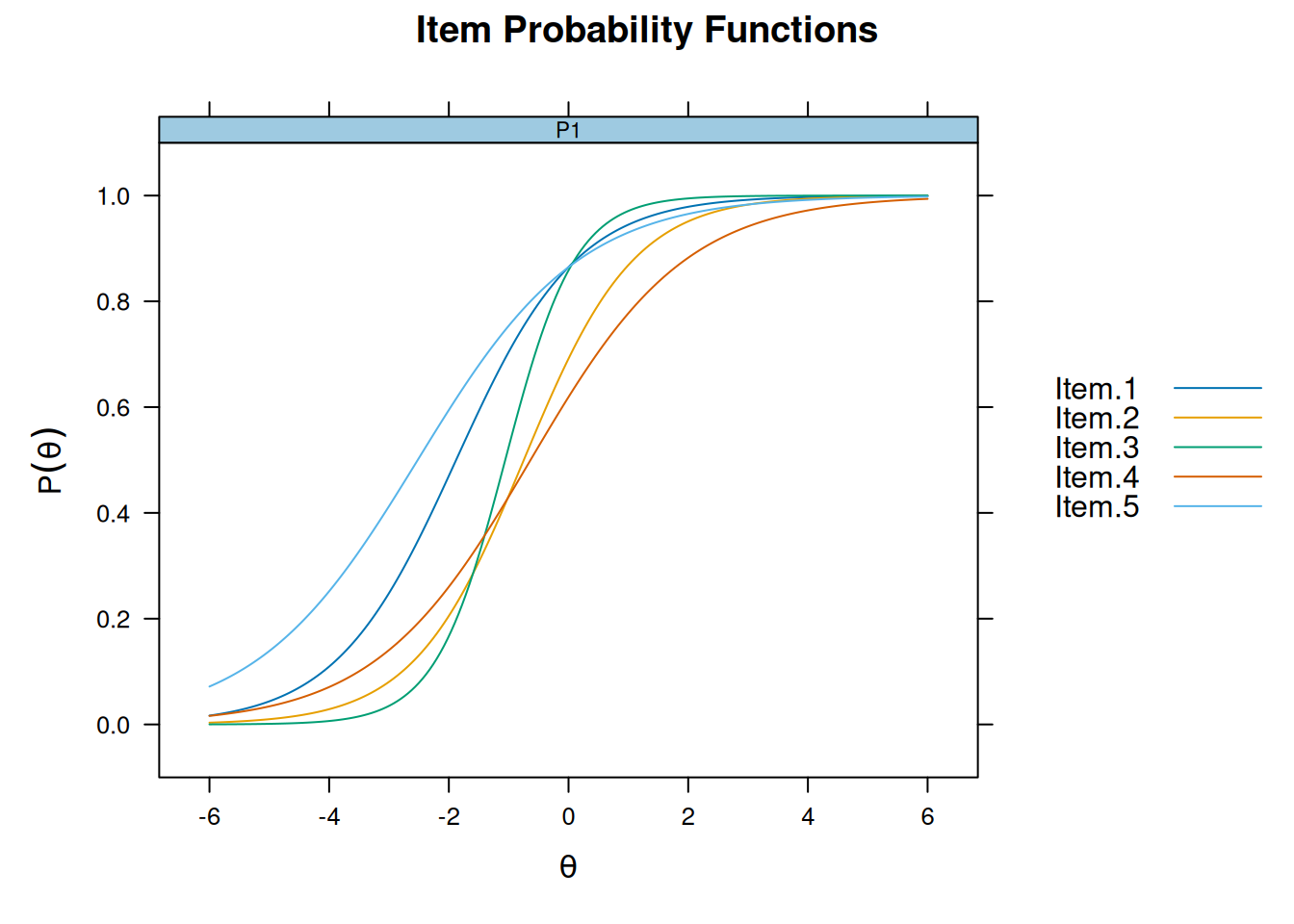
Plot the item information curve for the 2-PL model. Which item has the highest information at \(\theta = 0\)?

Your answer:

# Insert R code

Model Comparison

anova(m_rasch, m_2pl)

Some Polytomous Models

Rating scale model

data(bfi, package = "psych")
# Neuroticism
m_rsm <- mirt(bfi[16:20], itemtype = "rsm")


Iteration: 1, Log-Lik: -23985.274, Max-Change: 1.00910
Iteration: 2, Log-Lik: -22434.284, Max-Change: 0.18792
Iteration: 3, Log-Lik: -22338.797, Max-Change: 0.17826
Iteration: 4, Log-Lik: -22282.201, Max-Change: 0.12715
Iteration: 5, Log-Lik: -22244.160, Max-Change: 0.09083
Iteration: 6, Log-Lik: -22217.562, Max-Change: 0.06646
Iteration: 7, Log-Lik: -22198.665, Max-Change: 0.04953
Iteration: 8, Log-Lik: -22185.225, Max-Change: 0.03738
Iteration: 9, Log-Lik: -22175.730, Max-Change: 0.02839
Iteration: 10, Log-Lik: -22169.095, Max-Change: 0.02270
Iteration: 11, Log-Lik: -22164.507, Max-Change: 0.01858
Iteration: 12, Log-Lik: -22161.370, Max-Change: 0.01513
Iteration: 13, Log-Lik: -22156.185, Max-Change: 0.01992
Iteration: 14, Log-Lik: -22155.234, Max-Change: 0.00485
Iteration: 15, Log-Lik: -22155.115, Max-Change: 0.00311
Iteration: 16, Log-Lik: -22154.996, Max-Change: 0.00344
Iteration: 17, Log-Lik: -22154.963, Max-Change: 0.00141
Iteration: 18, Log-Lik: -22154.950, Max-Change: 0.00099
Iteration: 19, Log-Lik: -22154.935, Max-Change: 0.00132
Iteration: 20, Log-Lik: -22154.930, Max-Change: 0.00040
Iteration: 21, Log-Lik: -22154.929, Max-Change: 0.00027
Iteration: 22, Log-Lik: -22154.928, Max-Change: 0.00033
Iteration: 23, Log-Lik: -22154.928, Max-Change: 0.00012
Iteration: 24, Log-Lik: -22154.928, Max-Change: 0.00008

itemfit(m_rsm, na.rm = TRUE)  # not fitting well

Sample size after row-wise response data removal: 2694

plot(m_rsm, type = "trace")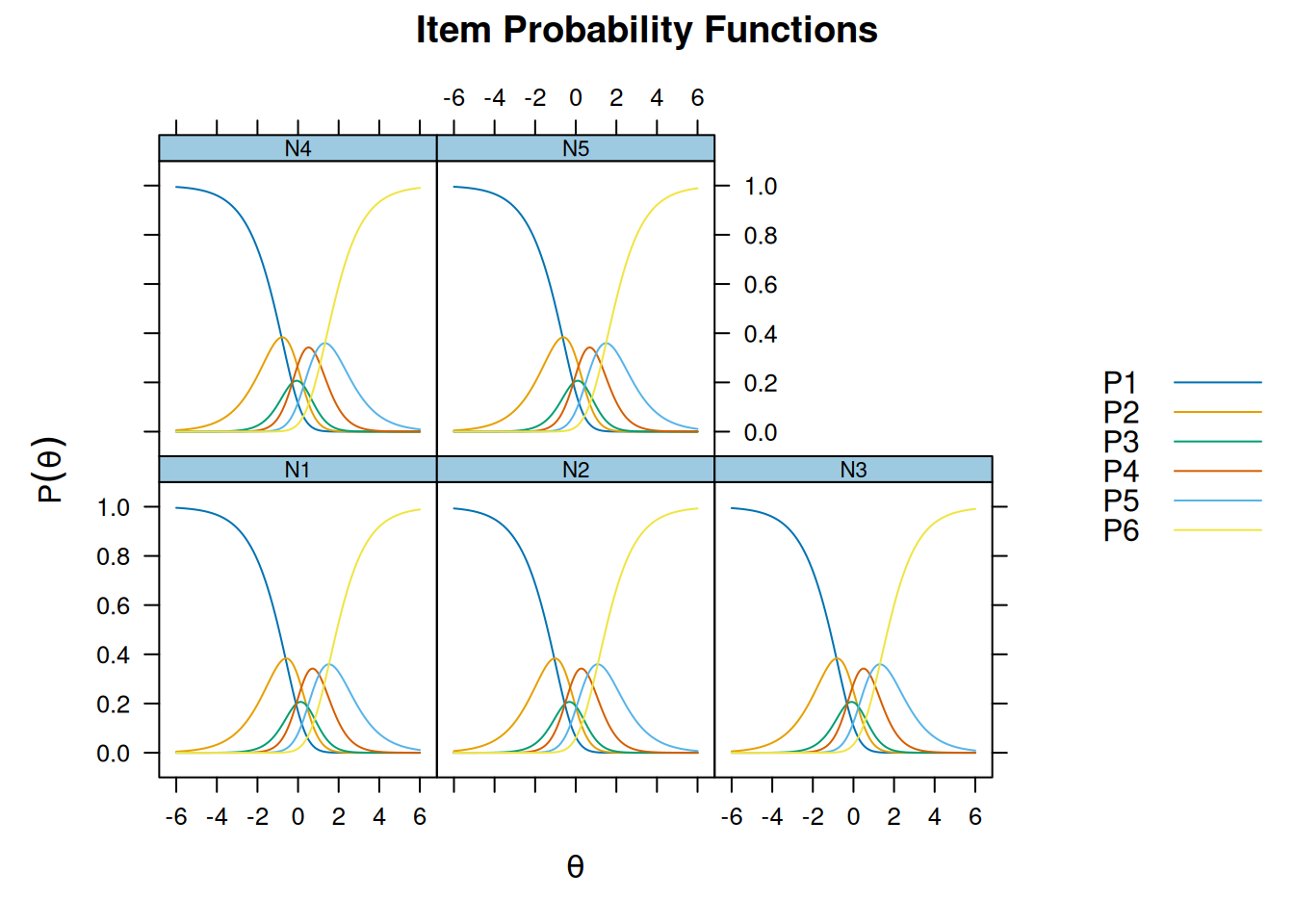

Graded Response model

m_grm <- mirt(bfi[16:20], itemtype = "graded")


Iteration: 1, Log-Lik: -22678.849, Max-Change: 0.98180
Iteration: 2, Log-Lik: -22009.516, Max-Change: 0.62057
Iteration: 3, Log-Lik: -21843.393, Max-Change: 0.31998
Iteration: 4, Log-Lik: -21773.416, Max-Change: 0.25006
Iteration: 5, Log-Lik: -21747.311, Max-Change: 0.16264
Iteration: 6, Log-Lik: -21734.951, Max-Change: 0.15148
Iteration: 7, Log-Lik: -21728.377, Max-Change: 0.09627
Iteration: 8, Log-Lik: -21724.841, Max-Change: 0.07974
Iteration: 9, Log-Lik: -21722.917, Max-Change: 0.06180
Iteration: 10, Log-Lik: -21721.933, Max-Change: 0.02070
Iteration: 11, Log-Lik: -21721.615, Max-Change: 0.01547
Iteration: 12, Log-Lik: -21721.511, Max-Change: 0.01199
Iteration: 13, Log-Lik: -21721.392, Max-Change: 0.00246
Iteration: 14, Log-Lik: -21721.388, Max-Change: 0.00214
Iteration: 15, Log-Lik: -21721.385, Max-Change: 0.00159
Iteration: 16, Log-Lik: -21721.382, Max-Change: 0.00202
Iteration: 17, Log-Lik: -21721.381, Max-Change: 0.00050
Iteration: 18, Log-Lik: -21721.381, Max-Change: 0.00008

itemfit(m_grm, na.rm = TRUE)  # not fitting well

Sample size after row-wise response data removal: 2694

plot(m_grm, type = "trace")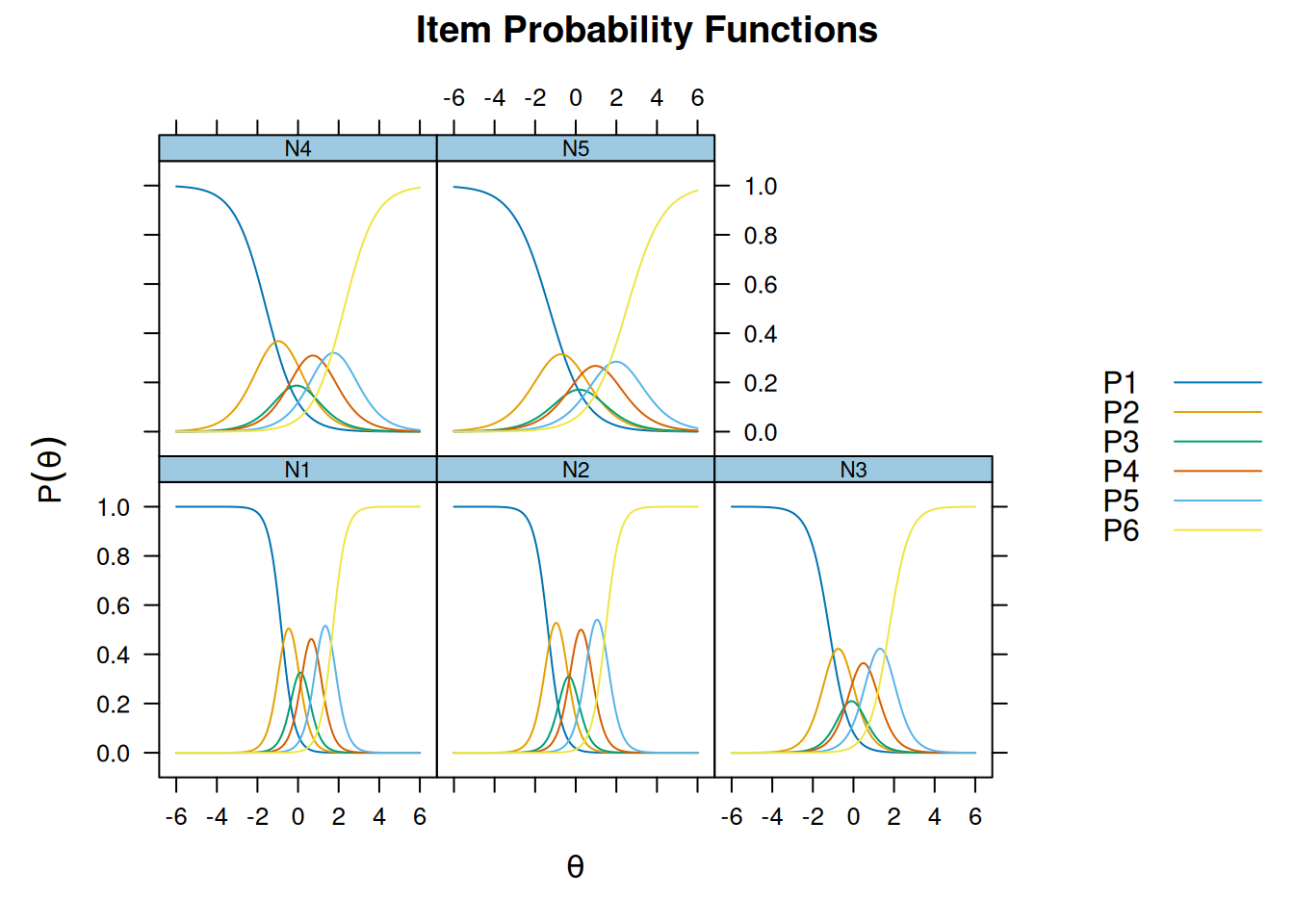

plot(m_grm, type = "info")