6 Poisson Model

Please note: This document uses count data on fatal police shootings.

I came across this data set from https://andrewpwheeler.com/2021/01/11/checking-a-poisson-distribution-fit-an-example-with-officer-involved-shooting-deaths-wapo-data-r-functions/

As explained here, the data are by the Washington Post in an effort to record every fatal shooting in the United States by a police officer since January 1, 2015.

6.1 Research Question

What’s the rate of fatal police shootings in the United States per year?

6.2 Data Import and Pre-Processing

# Import data
fps_dat <- read_csv(
    "https://github.com/washingtonpost/data-police-shootings/raw/master/v2/fatal-police-shootings-data.csv"
)

We first count the data by year

# Create a year column
fps_dat <- fps_dat |>
    mutate(year = format(date, format = "%Y"))
# Filter out the latest year
fps_1523 <- filter(fps_dat, year != max(year))
count(fps_1523, year)

Our interest is the rate of occurrence of fatal police shootings per year. Denote this as \(\theta\). The support of \(\theta\) is \([0, \infty)\).

A Poisson model is usually a starting point for analyzing count data in a fixed amount of time. It assumes that the data follow a Poisson distribution with a fixed rate parameter: \[P(y \mid \theta) \propto \theta^y \exp(- \theta),\] where the data can be any non-negative integers (no decimals).

6.3 Choosing a Prior

The Gamma distribution has support: \([0, \infty)\), and is a conjugate family to the Poisson model. The Gamma distribution has the form \[ P(\theta) \propto \theta^{a - 1} \exp(-b \theta), \] where \(a\) is the prior incidence rate, and \(b\) is the number of prior data points to control for the prior strength. Here, without much prior knowledge, I would simply guess there is one fatal shooting per state per month, so 600 shootings per year, but my belief is pretty weak, so I will assume a prior \(b\) of 1 / 200 (one observation is one year). The \(a\) will be 600 * \(b\) = 3.

Here’s a plot:

ggplot(data.frame(th = c(0, 2000)), aes(x = th)) +
    stat_function(fun = dgamma,
    args = list(shape = 3, rate = 1 / 200)) +
    labs(y = "", x = expression(theta))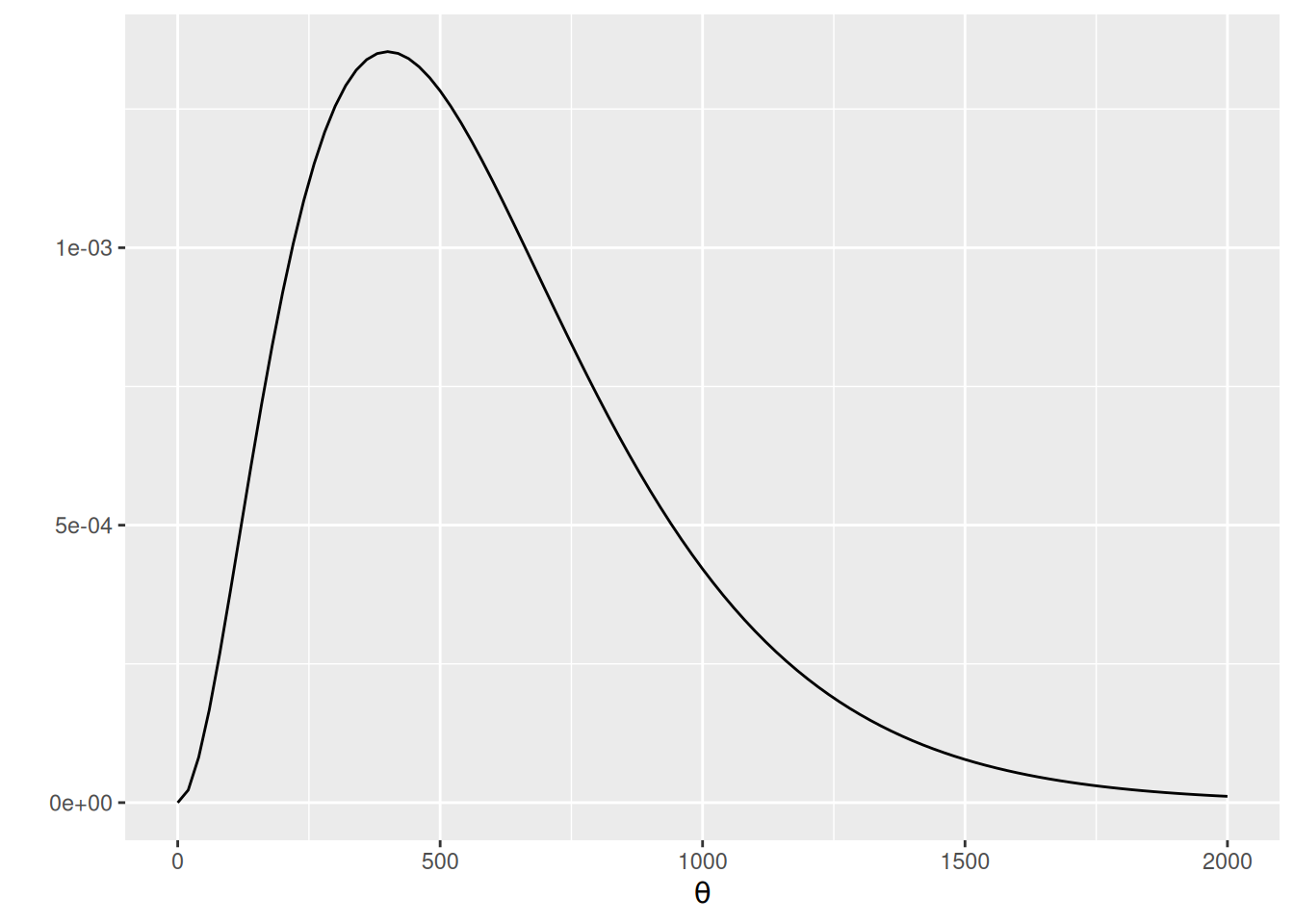

Model Fitting in Stan

data {
  int<lower=0> N;  // number of observations
  array[N] int<lower=0> y;  // y
  real<lower=0> prior_a;  // prior a for gamma
  real<lower=0> prior_b;  // prior b for gamma
}
parameters {
  real<lower=0> theta;  // theta parameter
}
model {
  // prior: Gamma(3, 1 / 200)
  // using conjugacy
  theta ~ gamma(prior_a + sum(y), prior_b + N);
}
generated quantities {
  real prior_theta = gamma_rng(3, 0.005);
  array[N] int prior_ytilde;
  array[N] int ytilde;
  for (i in 1:N) {
    ytilde[i] = poisson_rng(theta);
    prior_ytilde[i] = poisson_rng(prior_theta);
  }
}

6.3.1 Compiling

pois_mod <- cmdstan_model("stan_code/gamma-poisson-pp.stan")

6.3.2 Data for Stan

fps_standata <- list(
    N = length(unique(fps_1523$year)),
    y = count(fps_1523, year)[, 2, drop = TRUE],  # integer
    prior_a = 3,
    prior_b = 1 / 200
)
fps_standata

$N
[1] 9

$y
[1]  995  959  984  992  994 1021 1050 1097 1164

$prior_a
[1] 3

$prior_b
[1] 0.005

6.3.3 MCMC Sampling

fit <- pois_mod$sample(
    fps_standata,
    refresh = 500  # show progress every 500 iterations
)

Running MCMC with 4 sequential chains...

Chain 1 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 1 Iteration:  500 / 2000 [ 25%]  (Warmup) 
Chain 1 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 1 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 1 Iteration: 1500 / 2000 [ 75%]  (Sampling) 
Chain 1 Iteration: 2000 / 2000 [100%]  (Sampling)

Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 1 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 1

Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 1 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 1

Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 1 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 1

Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 1 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 1

Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 1 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 1

Chain 1 finished in 0.0 seconds.
Chain 2 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 2 Iteration:  500 / 2000 [ 25%]  (Warmup) 
Chain 2 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 2 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 2 Iteration: 1500 / 2000 [ 75%]  (Sampling) 
Chain 2 Iteration: 2000 / 2000 [100%]  (Sampling)

Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 2 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 2

Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 2 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 2

Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 2 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 2

Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 2 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 2

Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 2 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 2

Chain 2 finished in 0.0 seconds.
Chain 3 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 3 Iteration:  500 / 2000 [ 25%]  (Warmup) 
Chain 3 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 3 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 3 Iteration: 1500 / 2000 [ 75%]  (Sampling) 
Chain 3 Iteration: 2000 / 2000 [100%]  (Sampling)

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3

Chain 3 finished in 0.0 seconds.
Chain 4 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 4 Iteration:  500 / 2000 [ 25%]  (Warmup) 
Chain 4 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 4 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 4 Iteration: 1500 / 2000 [ 75%]  (Sampling) 
Chain 4 Iteration: 2000 / 2000 [100%]  (Sampling)

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: gamma_lpdf: Random variable is inf, but must be positive finite! (in '/tmp/Rtmptr69JG/model-2756e8977df2.stan', line 13, column 2 to column 47)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4

Chain 4 finished in 0.0 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.0 seconds.
Total execution time: 0.6 seconds.

6.3.4 Prior predictive check

Here I plot simulated trends from the prior distribution.

# Extract predicted y from prior
fit$draws("prior_ytilde", format = "draws_matrix") |>
    ppd_intervals(x = 2015:2023) +
    labs(x = "Year", y = "Predicted count")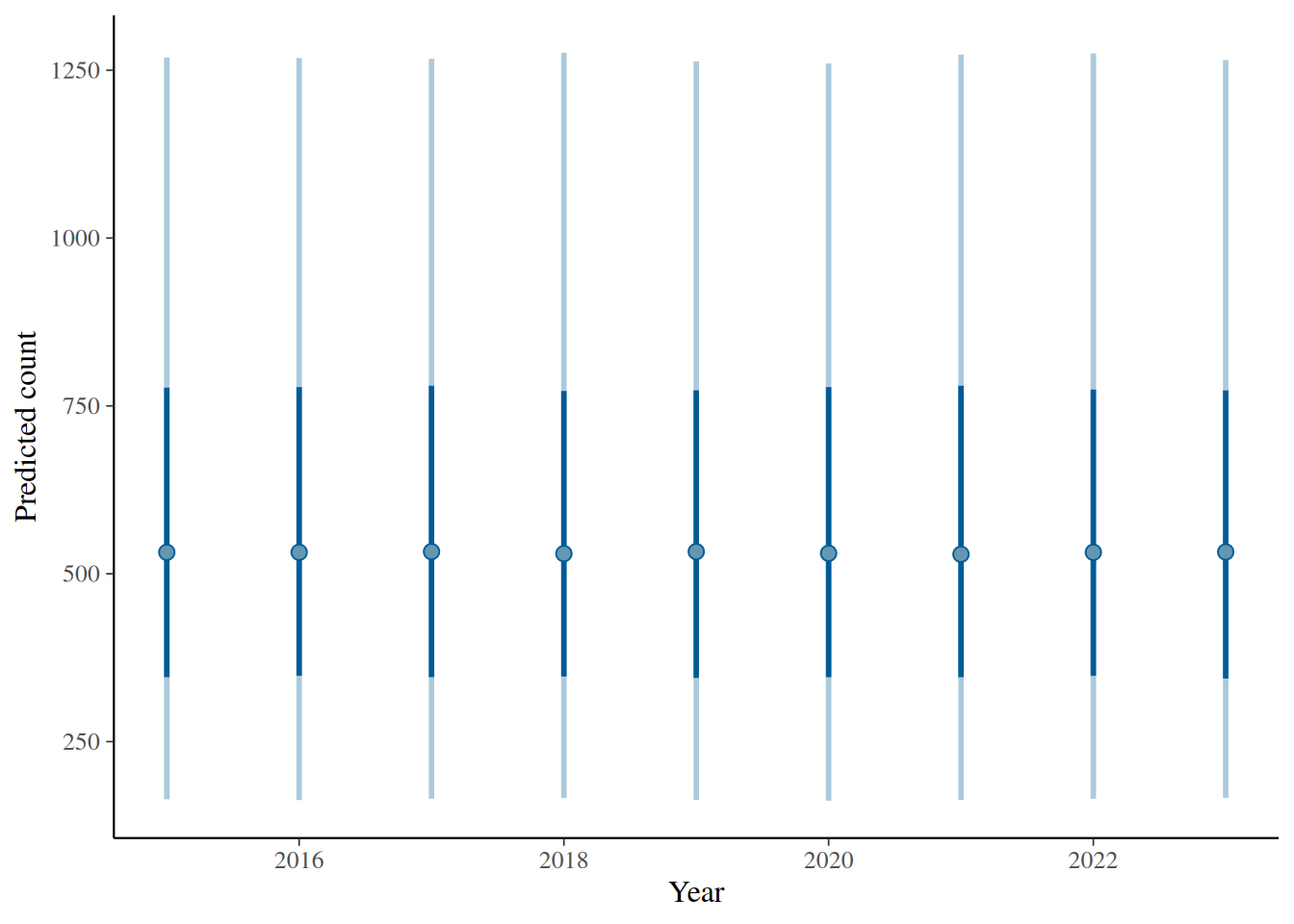

The check is on whether the numbers seem reasonably reflective of my knowledge.

6.4 Posterior

With a conjugate prior, the posterior distribution is Gamma(\(a\) + \(\sum_{i = 1}^N y_i\), \(b\) + \(N\)).

ggplot(data.frame(th = c(0, 2000)), aes(x = th)) +
    stat_function(fun = dgamma,
    args = list(shape = 3 + nrow(fps_1523),
                rate = 1 / 200 + fps_standata$N), n = 501) +
    labs(y = "", x = expression(theta))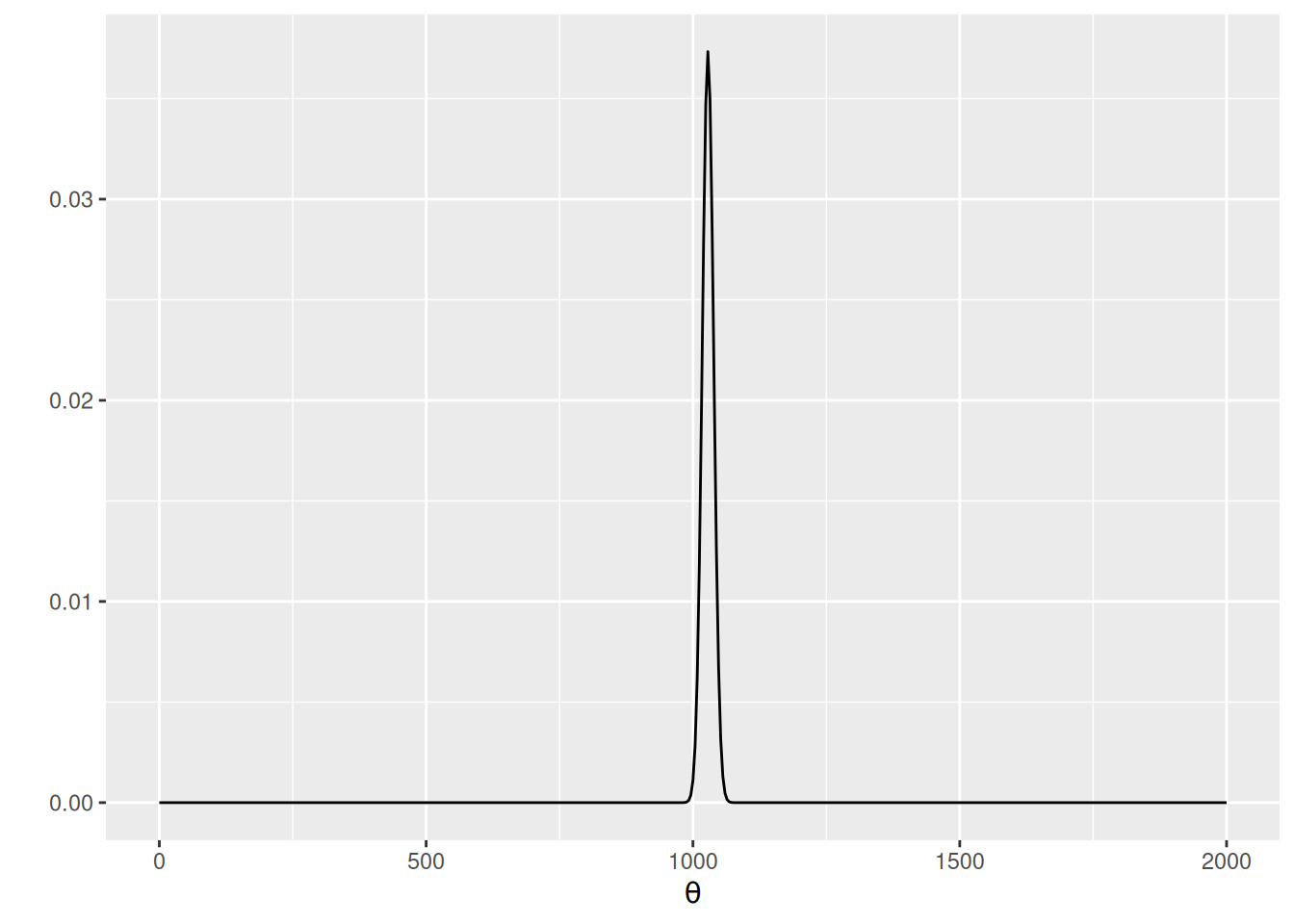

6.5 Posterior Predictive Check

Plot predicted data from the posterior against observed data

# Extract predicted y from posterior
fit$draws("ytilde", format = "draws_matrix") |>
    ppc_intervals(
        y = fps_standata$y,
        x = 2015:2023
    ) +
    labs(x = "Year", y = "Predicted count")
# We can also use `bayesplot::ppc_ribbon()`
fit$draws("ytilde", format = "draws_matrix") |>
    ppc_ribbon(
        y = fps_standata$y,
        x = 2015:2023
    ) +
    labs(x = "Year", y = "Predicted count")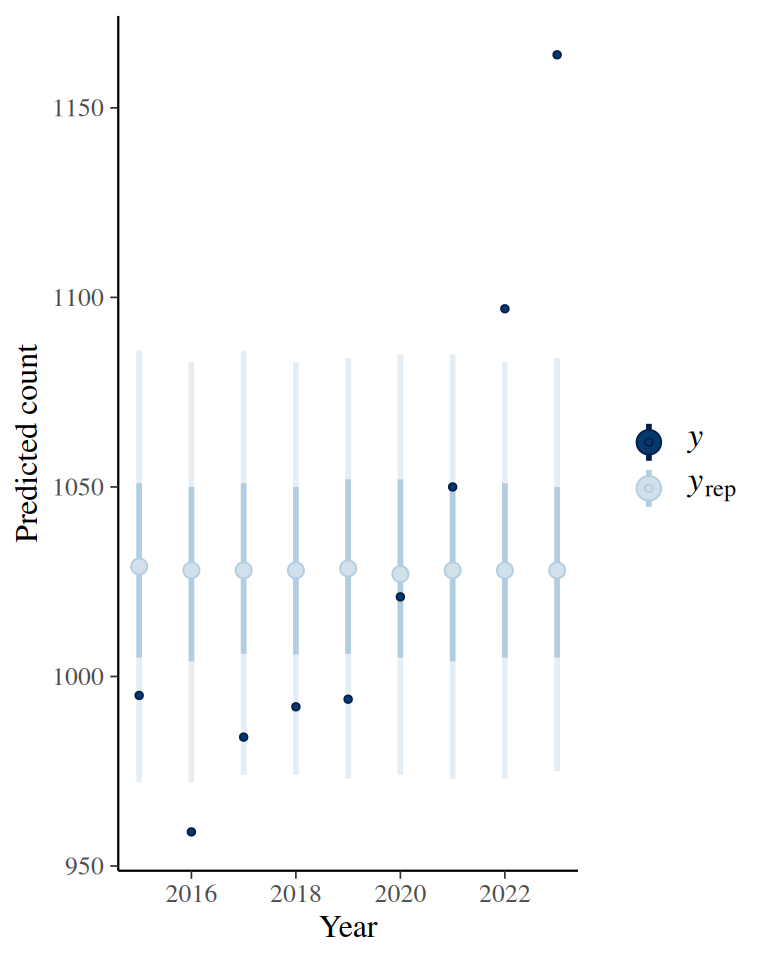

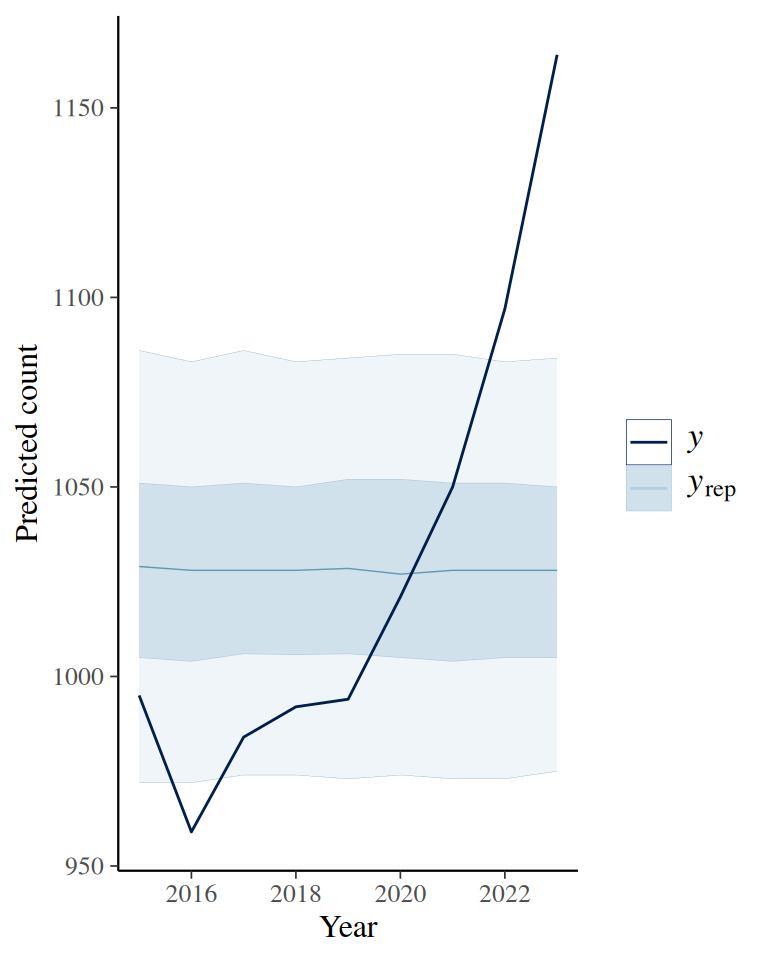
From Figure 6.1, one can see that the fit is not good, as there is a large gap between the model prediction and the observed data from recent years. This suggests a need to incorporate the time trend in the model.

6.6 Summary of Posterior

For now, we will proceed with interpreting the posterior distribution, despite the apparent misfit.

(summ_theta <- fit$summary("theta"))

So the estimated rate is 1,028 per year, with a 90% CI [1,011, 1,046].